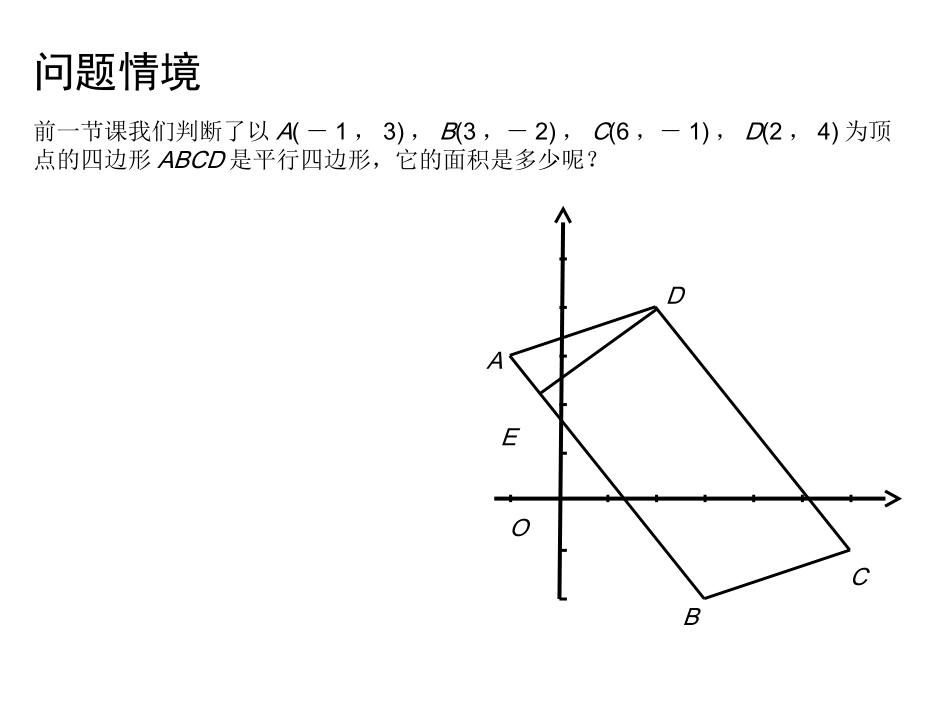
点到直线的距离前一节课我们判断了以A(-1,3),B(3,-2),C(6,-1),D(2,4)为顶点的四边形ABCD是平行四边形,它的面积是多少呢?问题情境OABCDE数学建构点到直线的距离点P(x0,y0)是平面上任意一点,直线l是平面上任意一直线,(1)直线l平行于x轴,记直线l的方程为y=b则点P到直线l的距离为(2)直线l平行于y轴,记直线l的方程为x=a,则点P到直线l的距离为(3)直线l与x轴、y轴都相交题型1点到直线的距离[典例1]求点P0(-1,2)到下列直线的距离:(1)2x+y-10=0;(2)x=2;(3)y-1=0..练习一(1)若点(a,2)到直线3x-4y-2=0的距离等于4,则a的值为______.(2)若点(4,0)到直线4x-3y+a=0的距离为3,则a的值为________.(3)点P是直线4x-3y-6=0任意一点,则点P到直线4x-3y+9=0的距离为________.题型2两平行直线的距离[典例2]求平行线2x-7y+8=0和2x-7y-6=0的距离.练习二(1)与两条平行直线2x+y+1=0和2x+y+5=0的距离相等的点的轨迹方程为__________.(2)两点A(1,0),B(3,4)到直线l的距离均等于1,则直线l的方程为___.(3)求与直线3x-4y+8=0平行且距离为2的直线方程.(4)若直线l1过点A(5,0),直线l2过点B(0,1),且l1//l2,l1和l2间的距离为5,求l1,l2的直线方程.题型3距离公式的综合应用[典例3]已知直线l经过直线l1:2x+y-5=0与l2:x-2y=0的交点.(1)若点A(5,0)到l的距离为3,求l的方程;(2)求点A(5,0)到l的距离的最大值.解:(1)法一:联立2x+y-5=0,x-2y=0⇒交点P(2,1),当直线斜率存在时,设l的方程为y-1=k(x-2),即kx-y+1-2k=0,所以|5k+1-2k|k2+(-1)2=3,解得k=43,所以l的方程为y-1=43(x-2),即4x-3y-5=0.而直线斜率不存在时直线x=2也符合题意,故所求l方程为4x-3y-5=0或x=2.法二:设经过两已知直线交点的直线系方程为(2x+y-5)+λ(x-2y)=0,即(2+λ)x+(1-2λ)y-5=0,所以|5(2+λ)-5|(2+λ)2+(1-2λ)2=3,即2λ2-5λ+2=0,解得λ=2或12,所以l方程为4x-3y-5=0或x=2.(2)由2x+y-5=0,x-2y=0,解得交点P(2,1),如图所示,过点P任意作直线l,设d为A到l的距离,则d≤PA(当l⊥PA时等号成立),所以dmax=PA=(5-2)2+(0-1)2=10.练习三已知点A(2,-1).(1)求过点A且与原点O距离为2的直线l的方程;(2)求过点A且与原点O距离最大的直线l的方程,最大距离是多少?解:(1)当斜率不存在时,直线l的方程为x=2,此时,原点O到直线l的距离为2,符合题意;当斜率存在时,可设直线l的方程为y+1=k(x-2),即kx-y-2k-1=0,由已知得|-2k-1|k2+1=2,解得k=34,此时直线l的方程为3x-4y-10=0.综上可知,直线l的方程为x=2或3x-4y-10=0.(2)过点A且与原点O距离最大的直线是过点A且与AO垂直的直线,由l⊥AO,得klkOA=-1,所以kl=-1kOA=2,所以直线l的方程为y+1=2(x-2),即2x-y-5=0,最大距离OA=(2-0)2+(-1-0)2=5,所以直线2x-y-5=0是过点A且与原点O距离最大的直线l的方程,最大距离为5.总结1.点P(x0,y0)到直线Ax+By+C=0的距离为_____________________.2.我们定义“夹在两条平行线间的公垂线段的长度称为两条平行线间的距离”.若两条平行线分别为l1:Ax+By+C1=0,l2:Ax+By+C2=0,则它们之间的距离为_________________.d=|Ax0+By0+C|A2+B2d=|C2-C1|A2+B2