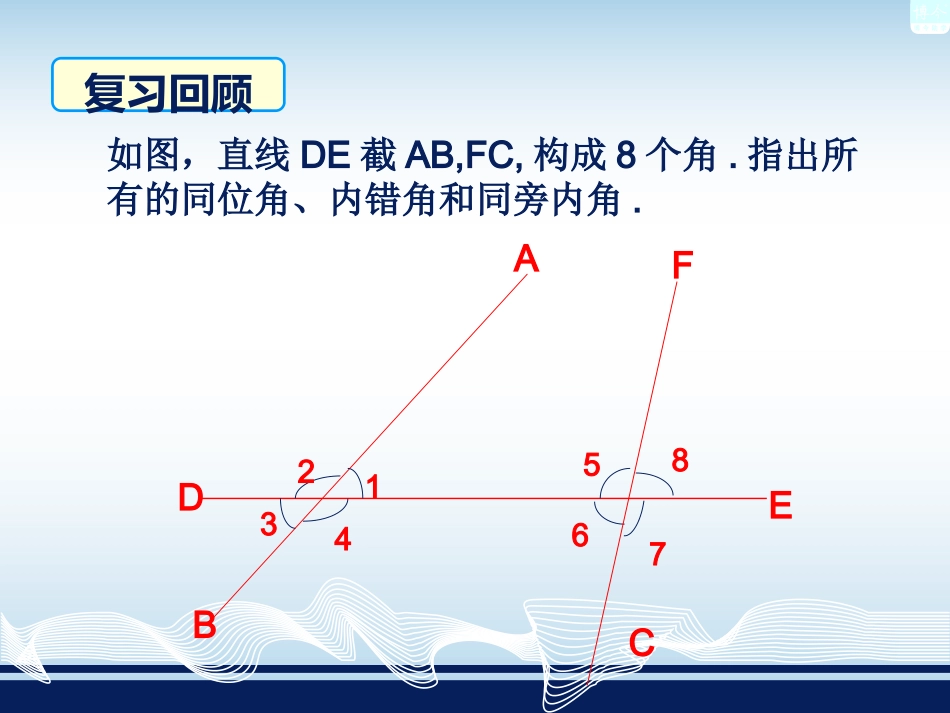
平行线的性质本课内容本节内容4.3问题1两条直线的位置关系有哪几种?问题2直线平行的定义是什么?问题3平行线有哪些定理和推论?相交、平行、重合.在同一平面内,不相交的两条直线平行.平行于同一条直线的两条直线平行.过直线外一点有且只有一条直线与这条直线平行.回顾与思考如图,直线DE截AB,FC,构成8个角.指出所有的同位角、内错角和同旁内角.12345678ABCDE复习回顾F做一做书在图4-20和图4-21中,AB∥CD,用量角器量下面两个图形中标出的角,填空:==你能猜想出什么结论?你能猜想出什么结论?猜想这个猜想对吗?这个猜想对吗?如果两条平行直线被第三条直线所截,那么同位角相等.探究如图4-22,直线AB,CD被直线EF所截,交于M,N两点,AB∥CD.作一个平移,移动方向为点M到点N的方向,移动距离等于线段MN的长度.则点M的像是,射线ME的像是.点N射线NE直线CD从而射线MB的像是.射线ND直线AB的像是,于是的像是,所以.ABCDEFMN一般地,平行线具有性质:性质1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.b12ac∴∠1=2∠(两直线平行,同位角相等)∵ab∥(已知)应用格式:结论如果两直线不平行,上述结论还成立吗?探究两条平行直线被第三条直线所截,内错角会具有怎样的数量关系?如图4-23,平行直线AB,CD被直线EF所截,∠1与∠2是内错角.分析:∵AB∥CD,∴∠1=∠4(两条直线平行,同位角相等).∵∠2=∠4(对顶角相等),∴∠1=∠2(等量代换).图4-23124ABCDFE性质2:两条平行线被第三条直线所截,内错角相等。简单说成:两直线平行,内错角相等.b12ac3∴∠2=∠3(两直线平行,内错角相等)∵ab∥(已知)应用格式:结论探究两条平行直线被第三条直线所截,同旁内角会具有怎样的数量关系?如图4-23,平行直线AB,CD被直线EF所截,∠1与∠3是同旁内角.分析:∵AB∥CD,∴∠1=∠4(两条平行直线被第三条直线所截,同位角相等).∵∠3+∠4=180o,∴∠1+∠3=180o(等量代换).图4-23134ABCDFE性质3:两条平行线被第三条直线所截,同旁内角互补。简单说成:两直线平行,同旁内角互补.b12ac4∴∠2+∠4=180°(两直线平行,同旁内角互补。)∵ab∥(已知)应用格式:结论结论平行线的三个性质可以简单的说成:两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.平行线的三个性质可以简单的说成:两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.举例例1如图4-24,直线AB,CD被直线EF所截,AB∥CD,∠1=100o,试求∠3的度数.图4-24解∵AB∥CD,∴∠1=∠2=100°(两直线平行,同位角相等).∵∠2+∠3=180°,∴∠3=180°-∠2=180°-100°=80°.123ABCDEF你还有别的方法来求证吗?利用同旁内角互补、对顶角相等4练1如图,a//b,∠3=60º,求∠4、∠5的度数.解:∵a∥b,∴∠3=4∠(两直线平行,内错角相等).∠5=180°-∠3=120°(两直线平行,同旁内角互补).45举例例2如图4-25,AD∥BC,∠B=∠D,试问∠A与∠C相等吗?为什么?图4-25解∵AB∥CD,∴∠A+∠B=180o,∠D+∠C=180o(两直线平行,同旁内角互补).又因为∠B=∠D(已知),所以∠A=∠C.ABCD练习如图,直线AB,CD被直线AE所截,AB∥CD,∠1=105°.求∠2,∠3,∠4的度数.(第2题图)1234ABCDE练习(第2题图)1234ABCDE解∵AB∥CD,∴∠1=∠2=105°(两直线平行,内错角相等).如图,直线AB,CD被直线AE所截,AB∥CD,∠1=105°.求∠2,∠3,∠4的度数.练习(第2题图)1234ABCDE解∵AB∥CD,∴∠1+∠3=180°(两直线平行,同旁内角互补).∴∠3=180°-∠1=180°-105°=75°.如图,直线AB,CD被直线AE所截,AB∥CD,∠1=105°.求∠2,∠3,∠4的度数.练习(第2题图)1234ABCDE解∵AB∥CD,∴∠1=∠4=105°(两直线平行,同位角相等).如图,直线AB,CD被直线AE所截,AB∥CD,∠1=105°.求∠2,∠3,∠4的度数.小结平行线的性质是什么?平行线的性质是什么?平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.作业:书P88习题4.31、3思考:如图,已知a//b,直线c与直线a、b相交于C、D两点,把一块含30°角的三角尺如图放置,若∠1=130°,求∠2的度数。abcCABD12∠2=20°3