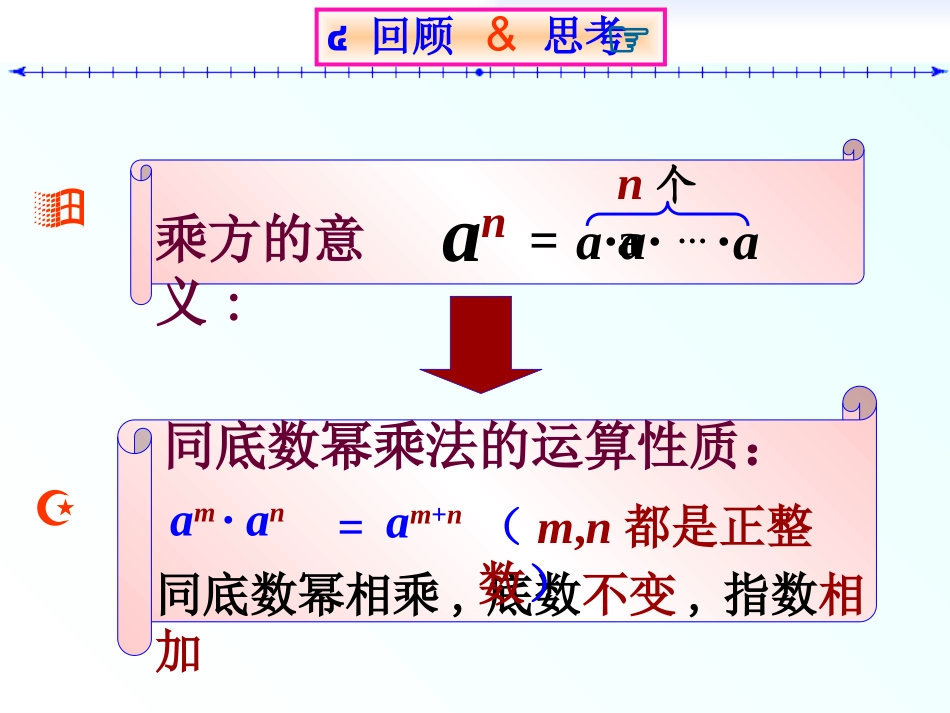
340Km430Km同底数幂乘法的运算性质:am·an=回顾与思考๔回顾&思考☞an乘方的意义:a·a·…·an个a=同底数幂相乘,底数不变,指数相加am+n(m,n都是正整数)ana·a·…·an个a=(102)n=102×102×···×102n个102(bm)5(x3)2=x3·x3幂的乘方:几个相同的幂相乘的运算.(am)n读作:a的m次幂的n次方表示:n个am相乘,=bm·bm·bm·bm·bm5个bm=a5m;做一做做一做根据乘方的意义及同底数幂的乘法计算:(1)(23)2;(2)(a4)3;(3)(am)5;(1)(23)2(2)(a4)3(3)(am)5=26=a4·a4·a4=a4+4+4=a12=am·am·am·am·am=am+m+m+m+m=23×2;(23)2=a4×3;(a4)3=a5m;(am)5猜想(am)n=amn=23+3=23×23从上面的计算中,你发现了什么规律?(am)n=_________=_________=amn(am)n=amn(m,n都是正整数)底数,指数.幂的乘方,幂的乘方运算性质不变相乘例题解析【例1】计算:(1)(106)2;(2)(am)4(m是正整数);(3)-(y3)2;(4)(-y2)3;(5)(a2n-1)2(n是正整数);(6)[(x-y)3]2当幂的底数是多项式时,要注意作为一个整体.负数的奇次幂是负数,负数的偶次幂是正数1、计算(1)(104)4;(2)(x5)4;(3)-(-a2)5;(4)(-23)202、下列计算中正确的个数有()①.am·a2=a2m②.(a3)2=a5③.x3·x2=x6④.(-a3)2.a4=a9(A)1个(B)2个(C)3个(D)0个注:幂的乘方法则与同底数幂的乘法法则的异同D(am)n=amn(m,n都是正整数)aman=am+n(m,n都是正整数)例2.(-a2)3+(-a3)2-a2·a3(1)x2·x4+(x3)2(2)(a3)3·(a4)3(3)-(m4)2+m5·m3(4)(-a3)5·(-a2)2练一练:3、填空(1)108=(104)()(2)b27=()9(3)a12=(a3)()=(a2)()=a3·a()amn=(am)()=(an)()注:幂的乘方公式的逆用:n2b3m469340Km430Km我的收获是……我的体会是……已知:m,n为正整数,且am=3,an=5求a3m+2n的值1、已知2m+3n=5m,n为正整数,求4m·8n的值2、解方程:9x=3x+1作业学案正面完成作业