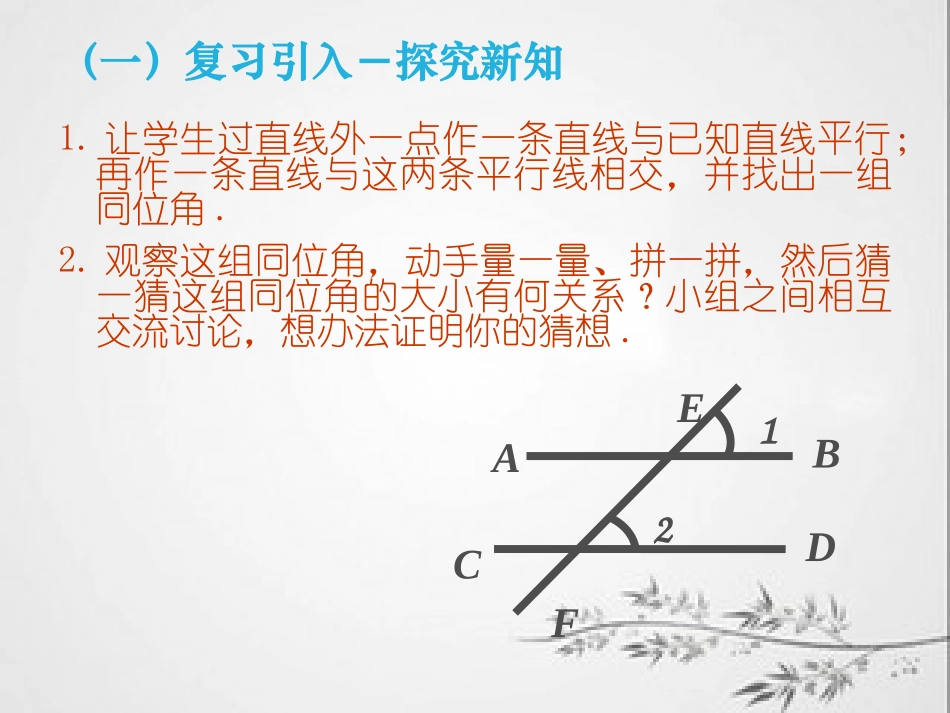
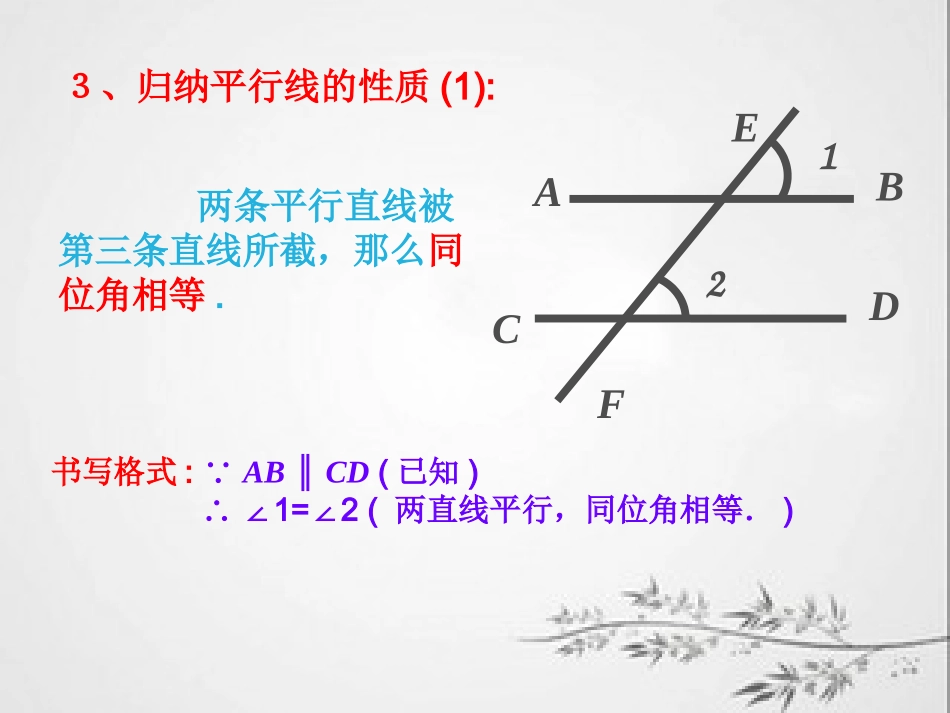
宜冲桥中学胡言军(一)复习引入-探究新知1.让学生过直线外一点作一条直线与已知直线平行;再作一条直线与这两条平行线相交,并找出一组同位角.2.观察这组同位角,动手量一量、拼一拼,然后猜一猜这组同位角的大小有何关系?小组之间相互交流讨论,想办法证明你的猜想.EBACDF123、归纳平行线的性质(1):EBACDF12两条平行直线被第三条直线所截,那么同位角相等.书写格式:∵AB∥CD(已知)∴∠1=2(∠两直线平行,同位角相等.)(二)说理证明-归纳性质再在前面图中分别找出一组内错角和同旁内角,试着用已学知识证明他们的大小关系,写出推理过程,得出结论并与同学在小组内进行讨论交流.B52ADEF2BACDEF3平行线的性质(2)两条平行直线被第三条直线所截,内错角相等.书写格式:∵AB∥CD(已知)∴∠5=2(∠两直线平行,内错角相等.)书写格式:∵AB∥CD(已知)∴∠3+2∠=180°(两直线平行,同旁内角互补.)平行线的性质(3):两条平行直线被第三条直线所截,同旁内角互补.(三)应用练习-巩固新知1、如图,已知平行线AB,CD被直线AE所截.??21101)1(为什么是多少度可以知道从??31101)2(为什么是多少度可以知道从??41101)3(为什么是多少度可以知道从2431ABCDE解:(1)ABCD∵∥∴∠2=1=110°(∠两直线平行,内错角相等)(2)ABCD∵∥∴∠3=1=110°(∠两直线平行,同位角相等)(3)ABCD∵∥∴∠4+1=180°(∠两直线平行,同旁内角互补)∴∠4=180°-∠1=180°-110°=70°2、如图,BE是AB的延长线,ADBC∥,ABCD∥,若∠D=100°,求∠C,∠A,∠CBE的度数。DBEAC解:∵ADBC∥∴∠C+D=180°(∠两直线平行,同旁内角互补)∴∠C=180°-∠D=180°-100°=80°∵ABCD∥∴∠A+D=180°(∠两直线平行,同旁内角互补)∴∠A=180°-∠D=180°-100°=80°∵ABCD∥∴AECD∥∴∠CBE=C=80°(∠两直线平行,内错角相等)87654321DCBAABCD3、如图,(1)若AD∥BC,则∠______=______,∠∠_______=_______,∠∠ABC+_______=180°;∠(2)若DC∥AB,则∠______=_______,∠∠______=_______,∠∠ABC+______=180°.∠8415BAD372BCD6(四)深思熟虑-回顾总结你有什么收获?困惑?友情提醒?2.如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是南偏西56°,甲、乙两地同时开工,若干天后公路准确接通,则乙地所修公路的走向是____,因为_________.56北乙甲北1.1∠和∠2是直线AB、CD被直线EF所截而成的内错角,那么∠1和∠2的大小关系是()A.1=2∠∠B.1>2∠∠C.1<2∠∠D.无法确定(五)当堂反馈-查漏补缺D北偏东56°两直线平行,内错角相等3.一个人驱车前进时,两次拐弯后,按原来的相反方向前进,这两次拐弯的角度是()A.向右拐85°,再向右拐95°;B.向右拐85°,再向左拐85°;C.向右拐85°,再向右拐85°;D.向右拐85°,再向左拐95°.4.如图,已知:DE∥CB,1=2,∠∠求证:CD平分∠ECB.E21DCBBCDEB解:∵DE∥CB∴∠1=BCD(∠两直线平行,内错角相等)∵∠1=2∠∴∠2=BCD(∠等量代换)∴CD平分∠ECB5、下列各图中,已知AB∥EF,点C任意选取(在AB、EF之间,又在BF的左侧).试猜想∠B、∠F、∠C之间的关系,写出这种关系,试加以说明.ABEFCFECBAABCEF课堂评价本节课教师的角色主要是学生学习的组织者、引导者。教师对学生的思维活动干预较少,学生不是停留在学会课本知识的层面上,而是站在研究者的角度深入其境。在设计上,强调自主学习,注重合作交流,从而探究总结出平行线的性质,感受到学习的乐趣,真正成为学习的主人,达到突出重点、突破难点的目的。以上是我对本节课的设计和说明,请各位同仁批评指正,谢谢大家!