弧、弦、圆心角、圆周角—知识讲解(提高)VIP免费

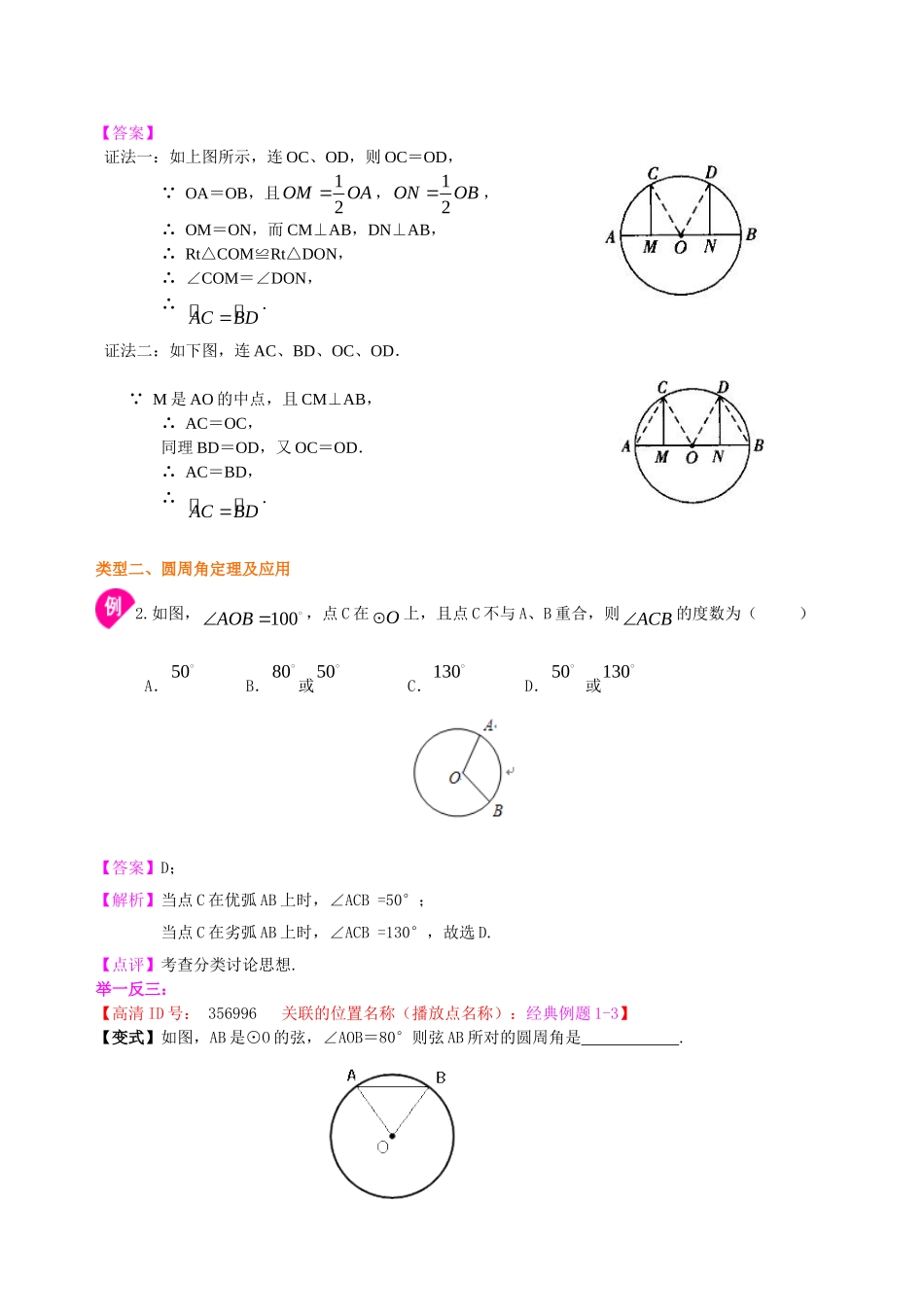
弧、弦、圆心角、圆周角—知识讲解（提高）【学习目标】1.了解圆心角、圆周角的概念；2.理解圆周角定理及其推论，能灵活运用圆周角的定理及其推理解决有关问题；3.掌握在同圆或等圆中，三组量：两个圆心角、两条弦、两条弧，只要有一组量相等，就可以推出其它两组量对应相等，及其它们在解题中的应用．【要点梳理】知识点一、弧、弦、圆心角的关系1.圆心角定义如图所示，∠AOB的顶点在圆心，像这样顶点在圆心的角叫做圆心角．2.定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．3.推论：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦也相等．在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧也相等．要点诠释：(1)一个角要是圆心角，必须具备顶点在圆心这一特征.(2)注意定理中不能忽视“同圆或等圆”这一前提.知识点二、圆周角1.圆周角定义：像图中∠AEB、∠ADB、∠ACB这样的角，它们的顶点在圆上，并且两边都与圆相交的角叫做圆周角．2.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．3.圆周角定理的推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．要点诠释：(1)圆周角必须满足两个条件：①顶点在圆上；②角的两边都和圆相交.(2)圆周角定理成立的前提条件是在同圆或等圆中.4.圆内接四边形：（1）定义:圆内接四边形：顶点都在圆上的四边形，叫圆内接四边形．（2）性质：圆内接四边形对角互补，外角等于内对角（即它的一个外角等于它相邻内角的对角）．5.弦、弧、圆心角、弦心距的关系：在同圆或等圆中，弦，弧，圆心角，弦心距等几何量之间是相互关联的，即它们中间只要有一组量相等，(例如圆心角相等)，那么其它各组量也分别相等(即相对应的弦、弦心距以及弦所对的弧也分别相等).*如果它们中间有一组量不相等，那么其它各组量也分别不等.【典型例题】类型一、圆心角、弧、弦之间的关系及应用1.已知：如图所示，⊙O中弦AB＝CD．求证：AD＝BC．【答案与解析】证法一：如图①， AB＝CD，∴ABCD．∴，即ADBC，∴AD＝BC．证法二：如图②，连OA、OB、OC、OD， AB＝CD，∴∠AOB＝∠COD．∴∠AOB－∠DOB＝∠COD－∠DOB，即∠AOD＝∠BOC，∴AD＝BC．【点评】在同圆或等圆中，证两弦相等时常用的方法是找这两弦所对的弧相等或所对的圆心角相等，而图中没有已知的等弧和等圆心角，必须借助已知的等弦进行推理．本题主要是考查弧、弦、圆心角之间的关系，要证AD＝BC，只需证ADBC或证∠AOD＝∠BOC即可．举一反三：【变式】如图所示，已知AB是⊙O的直径，M、N分别是AO、BO的中点，CM⊥AB，DN⊥AB．求证：ACBD．【答案】证法一：如上图所示，连OC、OD，则OC＝OD， OA＝OB，且12OMOA，12ONOB，∴OM＝ON，而CM⊥AB，DN⊥AB，∴Rt△COM≌Rt△DON，∴∠COM＝∠DON，∴ACBD．证法二：如下图，连AC、BD、OC、OD． M是AO的中点，且CM⊥AB，∴AC＝OC，同理BD＝OD，又OC＝OD．∴AC＝BD，∴ACBD．类型二、圆周角定理及应用2.如图，100AOB，点C在O上，且点C不与A、B重合，则ACB的度数为（）A．50B．80或50C．130D．50或130【答案】D；【解析】当点C在优弧AB上时，∠ACB=50°；当点C在劣弧AB上时，∠ACB=130°，故选D.【点评】考查分类讨论思想.举一反三：【高清ID号：356996关联的位置名称（播放点名称）：经典例题1-3】【变式】如图，AB是⊙O的弦，∠AOB＝80°则弦AB所对的圆周角是.【答案】40°或140°.【高清ID号：356996关联的位置名称（播放点名称）：经典例题4-5】3.如图，AB是⊙O的直径，C、D、E都是⊙O上的点，则∠1+∠2=___________.【答案】90°.【解析】如图，连接OE，则【点评】把圆周角转化到圆心角.举一反三：【变式】如图，A、B、C、D是⊙O上的四点，且∠BCD=100°，求∠1（所对的圆心角）和∠BAD的大小．【答案】 ∠BCD和∠2分别是所对的圆周角和圆心角∴∠2=2∠BCD=200°又 ∠2+∠1=360°，∴∠1=160° ∠BAD和∠1分别是所对的圆周角和圆心角∴．4.已知，如图，⊙O上三点A、B、C，...