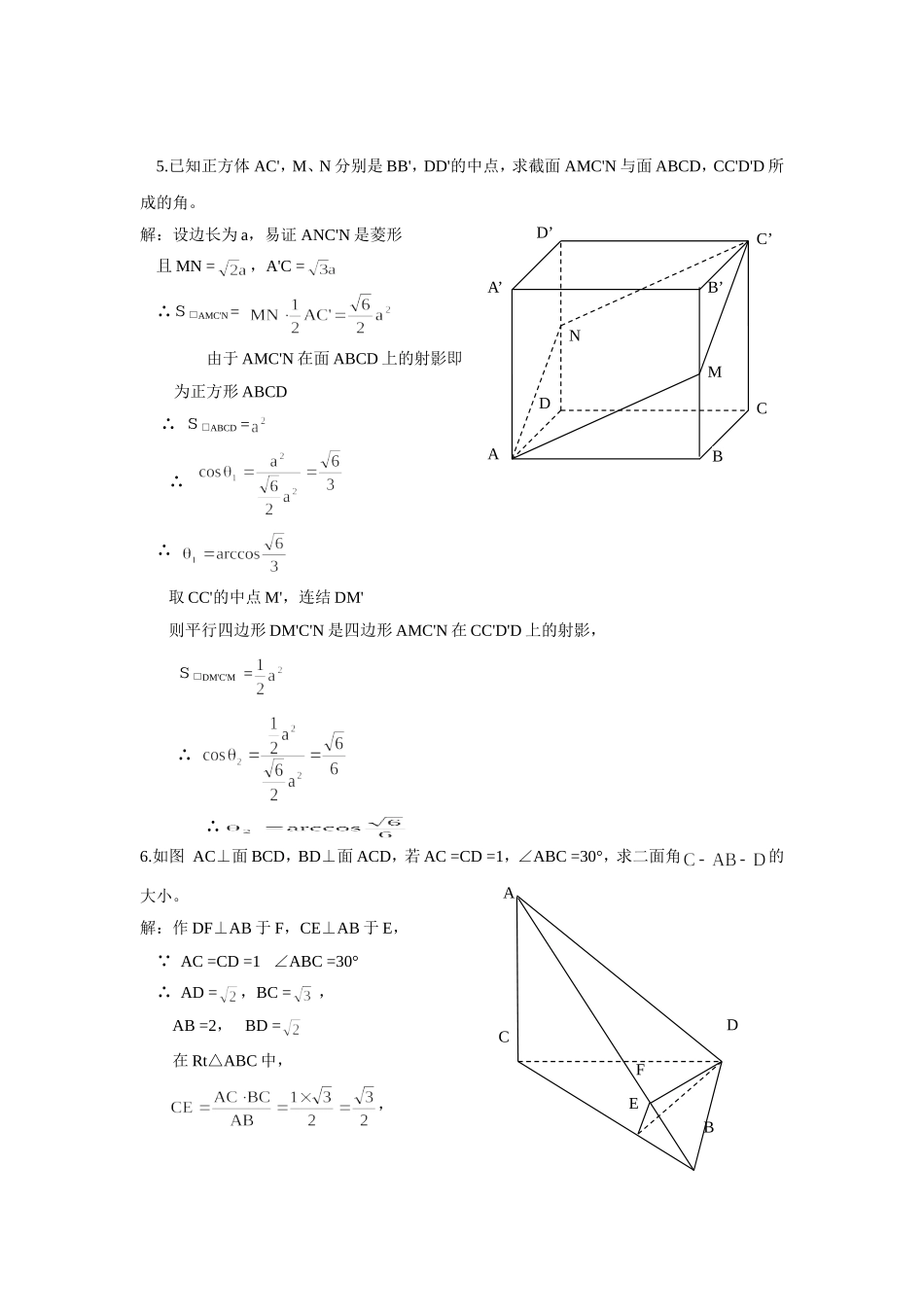
二面角1.如图三棱锥P-ABC中,PC⊥平面ABC,PC=,D是BC的中点,且△ADC是边长为2的正三角形,求二面角P-AB-C的大小。解:由已知条件,D是BC的中点∴CD=BD=2又△ADC是正三角形∴AD=CD=BD=2∴D是△ABC之外心又在BC上∴△ABC是以∠BAC为直角的三角形,∴AB⊥AC,又PC⊥面ABC∴PA⊥AB(三垂线定理)∴∠PAC即为二面角P-AB-C之平面角,易求∠PAC=30°2.如图在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于D、E,又SA=AB,BS=BC,求以BD为棱,BDE与BDC为面的二面角的度数。解:∵BS=BC,又DE垂直平分SC∴BE⊥SC,SC⊥面BDE∴BD⊥SC,又SA⊥面ABC∴SA⊥BD,BD⊥面SAC∴BD⊥DE,且BD⊥DC则∠EDC就是所要求的平面角设SA=AB=a,则BC=SB=a且AC=易证△SAC∽△DEC∴∠CDE=∠SAC=60°3.如图:ABCD是矩形,AB=8,BC=4,AC与BD相交于O点,P是平面ABCD外一点,PO⊥面ABCD,PO=4,M是PC的中点,求二面角M-BD-C大小。解:取OC之中点N,则MN∥PO∵PO⊥面ABCDDPCABEDBASCSRNMOBDPAC∴MN⊥面ABCD且MN=PO/2=2,过N作NR⊥BD于R,连MR,则∠MRN即为二面角M-BD-C的平面角过C作CE⊥BD于S则RN=CE在Rt△BCD中,CD·BC=BD·CE∴∴∴4.如图△ABC与△BCD所在平面垂直,且AB=BC=BD,∠ABC=∠DBC=,求二面角A-BD-C的余弦值。解:过A作AE⊥CB的延长线于E,连结DE,∵面ABC⊥面BCD∴AE⊥面BCD∴E点即为点A在面BCD内的射影∴△EBD为△ABD在面BCD内的射影设AB=a则AE=DE=ABsin60°=∴AD=,∴sin∠ABD=∴又∴∴考虑到我们求的是二面角A-BD-E,而二面角A-BD-C与A-BD-C互补∴二面角A-BD-C的余弦值为。DBAEC5.已知正方体AC',M、N分别是BB',DD'的中点,求截面AMC'N与面ABCD,CC'D'D所成的角。解:设边长为a,易证ANC'N是菱形且MN=,A'C=∴S□AMC'N=由于AMC'N在面ABCD上的射影即为正方形ABCD∴S□ABCD=∴∴取CC'的中点M',连结DM'则平行四边形DM'C'N是四边形AMC'N在CC'D'D上的射影,S□DM'C'M=∴∴6.如图AC⊥面BCD,BD⊥面ACD,若AC=CD=1,∠ABC=30°,求二面角的大小。解:作DF⊥AB于F,CE⊥AB于E,∵AC=CD=1∠ABC=30°∴AD=,BC=,AB=2,BD=在Rt△ABC中,,D’B’DAC’BA’CMNBFEACD同理∴∴∴∴即所求角的大小为。