函数的单调性与导数VIP免费

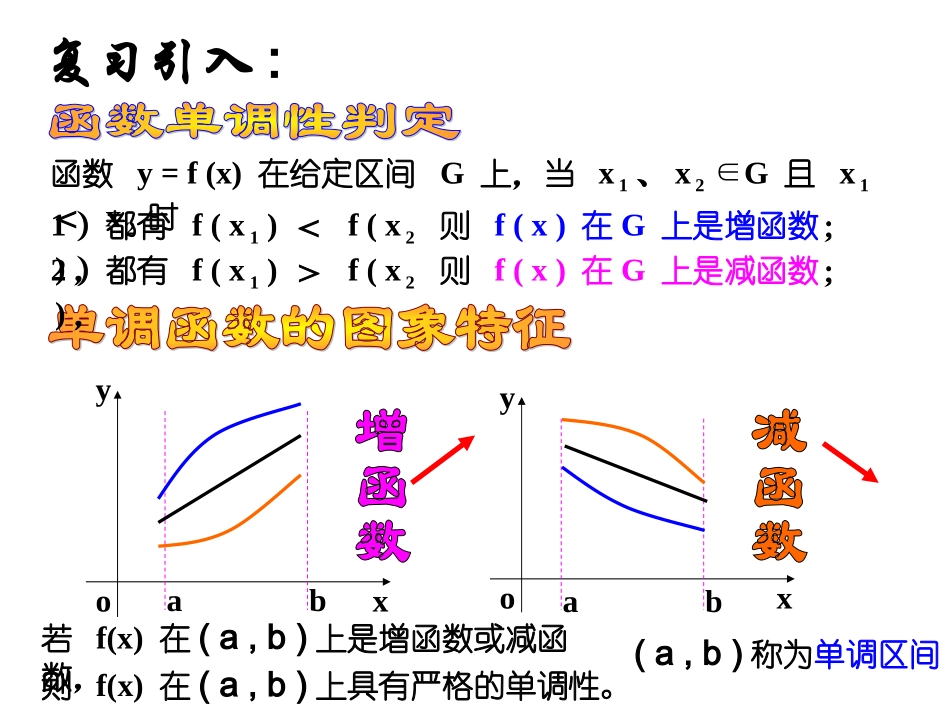
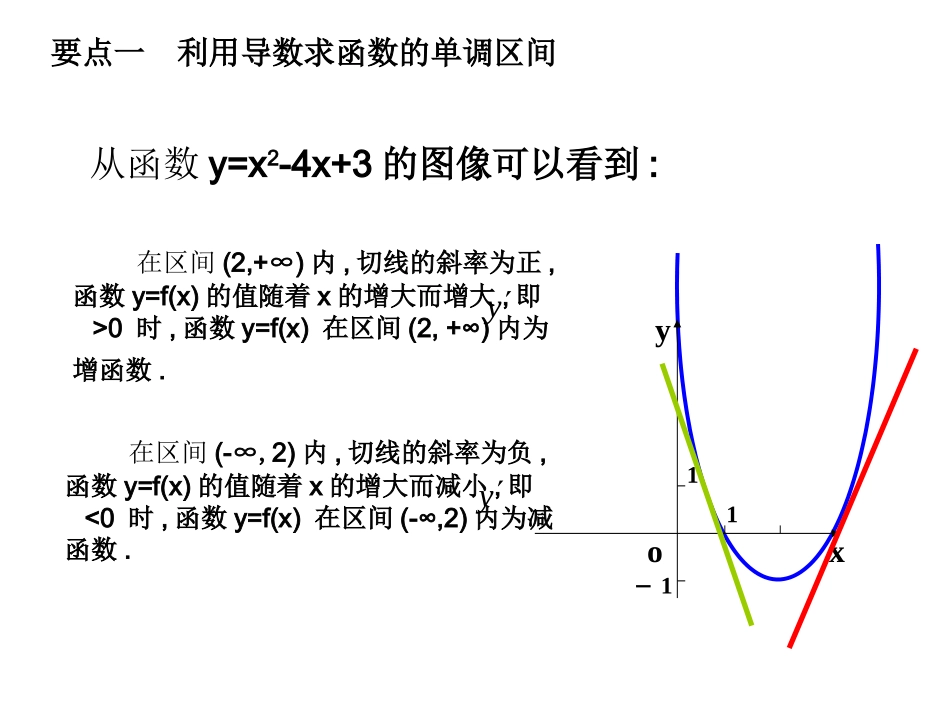
函数的单调性与导数函数y=f(x)在给定区间G上，当x1、x2G∈且x1＜x2时yxoabyxoab1）都有f(x1)＜f(x2)，则f(x)在G上是增函数；2）都有f(x1)＞f(x2)，则f(x)在G上是减函数；若f(x)在(a,b)上是增函数或减函数，则f(x)在(a,b)上具有严格的单调性。(a,b)称为单调区间复习引入:从函数y=x2-4x+3的图像可以看到:yxo11－1在区间(2,+∞)内,切线的斜率为正,函数y=f(x)的值随着x的增大而增大,即>0时,函数y=f(x)在区间(2,+∞)内为增函数.y在区间(-∞,2)内,切线的斜率为负,函数y=f(x)的值随着x的增大而减小,即<0时,函数y=f(x)在区间(-∞,2)内为减函数.y要点一利用导数求函数的单调区间aby=f(x)xoyy=f(x)xoyabf'(x)>0f'(x)<0定义:一般地,设函数y=f(x)在某个区间（a，b）内有导数,如果在这个区间内>0,那么函数在为这个区间内的增函数;如果在这个区间内<0,那么函数在为这个区间内的减函数.由上我们可得以下的结论:如果在某个区间内恒有,则为常数.0)(xf)(xf)(xf)(xf)(xfy)(xfy函数的单调性与导数的关系(1)在区间(a，b)内函数的导数与单调性有如下关系：导数函数的单调性f′(x)>0单调递___f′(x)<0单调递___f′(x)＝0常函数增减例1:讨论f(x)=x3-6x2+9x-3的单调性.10331yx故f(x)在(-∞,1)和(3,+∞)内是增函数,在(1,3)内是减函数.利用导数求函数f(x)的单调区间的一般步骤为:(1)确定函数f(x)的定义域；(2)求导数f′(x)；(3)在函数f(x)的定义域内解不等式f′(x)＞0和f′(x)＜0；(4)根据(3)的结果确定函数f(x)的单调区间.当堂练习：做练习册13页例2要点二利用导数判断函数的单调性例2证明：函数f(x)＝sinxx在区间π2，π上单调递减．证明f′(x)＝xcosx－sinxx2，又x∈π2，π，则cosx<0，sinx＞0，∴xcosx－sinx<0，∴f′(x)<0，∴f(x)在π2，π上是减函数．3xy032xy函数在R上递增(2)在区间(a，b)内函数的单调性与导数有如下关系：函数的单调性导数单调递增f′(x)____0单调递减f′(x)____0常函数f′(x)＝0≥≤要点三已知函数单调性求参数的取值范围例3已知函数f(x)＝x2＋ax(x≠0，常数a∈R)．若函数f(x)在x∈[2，＋∞)上是单调递增的，求a的取值范围．解f′(x)＝2x－ax2＝2x3－ax2.要使f(x)在[2，＋∞)上是单调递增的，则f′(x)≥0在x∈[2，＋∞)时恒成立，即2x3－ax2≥0在x∈[2，＋∞)时恒成立．∵x2>0，∴2x3－a≥0，∴a≤2x3在x∈[2，＋∞)上恒成立．∴a≤(2x3)min.∵x∈[2，＋∞)，y＝2x3是单调递增的，∴(2x3)min＝16，∴a≤16.当a＝16时，f′(x)＝2x3－16x2≥0(x∈[2，＋∞))有且只有f′(2)＝0，∴a的取值范围是(－∞，16]．例4如图,水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度h与时间t的函数关系图象.(A)(B)(C)(D)htOhtOhtOhtO一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图象就比较“陡峭”(向上或向下);反之,函数的图象就“平缓”一些.如图,函数在或内的图象“陡峭”,在或内的图象“平缓”.)(xfy),0(b)0,(a),(b),(a练习2.函数的图象如图所示,试画出导函数图象的大致形状)(xfy)(xf