倍长中线法(加倍法)VIP免费

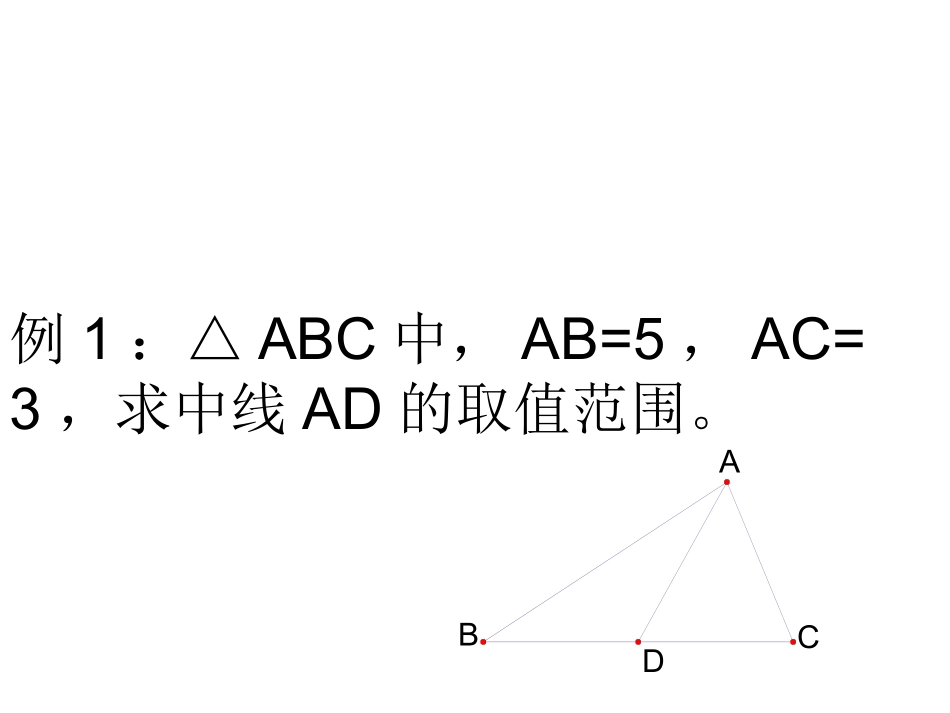
倍长中线法（加倍法）•知识网络详解：•中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．•所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．•倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS证全等（对顶角）•倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。例1：△ABC中，AB=5，AC=3，求中线AD的取值范围。DABC例2：已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且DF=EF，求证：BD=CEFECABD例3：已知在△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC，延长BE交AC于F，求证：AF=EFFEDABC例4：如图，AD为的中线，DE平分交AB于E，DF平分交AC于F.求证：EFCFBEDFCBEA例5：已知CD=AB，∠BDA=BAD∠，AE是△ABD的中线，求证：∠C=BAE∠EDABC1、如图，△ABC中，BD=DC=AC,E是DC的中点，求证，AD平分∠BAE。ABFDEC