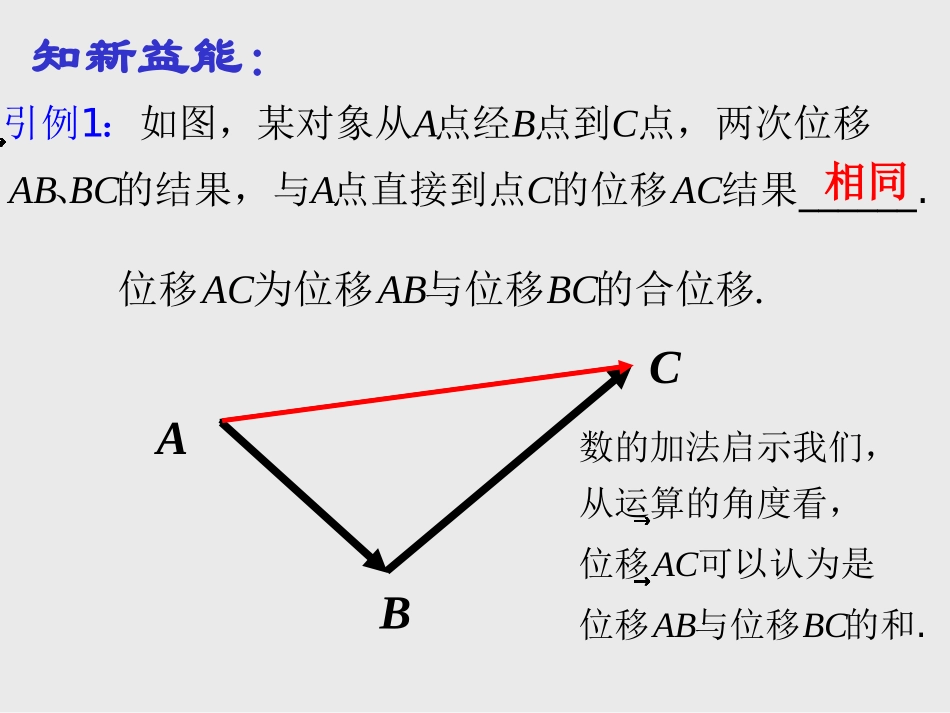
2.2.1平面向量加法运算及其几何意义1、向量:既有又有的量叫向量大小方向3、相等向量:长度且方向的向量叫相等向量2、共线向量(平行向量):(1)方向或_____的非零向量叫平行向量(2)规定:0//a相同相反相等相同温故夯基知新益能:ABC相同ABCABBCACAC�如图,某对象从点经点到点,两次位移、的结果,与点引直接到点的位移结果___例1:___..ACABBC�位移为位移与位移的合位移ACABBC��数的加法启示我们,从运算的角度看,位移可以认为是位移与位移的和.引例2:如图表示橡皮条在两个力作用下,沿着GC的方向伸长了EO。引例2:撤去和,用一个力作用在橡皮条上,使橡皮条沿着相同的方向伸长相同的长度.1F�2F�F�思考:力对橡皮条产生的效果,与力与共同作用的效果.相同1F�2F�F�12FFF��物理学中把力叫做与的合力F�改变力和的大小和方向,重复以上实验,观察力与,关系.1F�2F�1F�2F�12.FFF�可以认为是与的和即位移、力的合成可看作向量的加法.1、向量加法的定义abbbaACBa,,,,+abAABaBCbACabab���如图,已知向量、在平面内任取一点作则向量叫做与的和,记作非零,这种求向量和的方法,称为向量加法的三角形法则.求两个向量和的运算,叫做向量的加法.2、向量加法的三角形法则++.=abABBCAC��即两个向量的和是一个向量00aaa规定:OABCabbaOabOACBOOCab�以同一点为起点的两个已知向量、为邻边作,则以为起点的对角线就是与的和.3、向量加法的平行四边形法则?ab类比力的合成,我们还可以如何作出思考:abOAOBOC��即这种作向量和的方法叫做向量加法的平行四边形法则.abOBab�则OABaba法1:在平面内任取一点O,b典例分析OAa�作,ABb�OCOCab�连接,则法2:在平面内任取一点O,OAa�作,OBb�,OAOBOACB以、为邻边作OabbaCAB.abab例1.如图,已知向量、,求作向量小结1.一个定义--------2.两个法则--------作业课本91页第1题、第2题向量加法的定义三角形法则和平行四边形法则