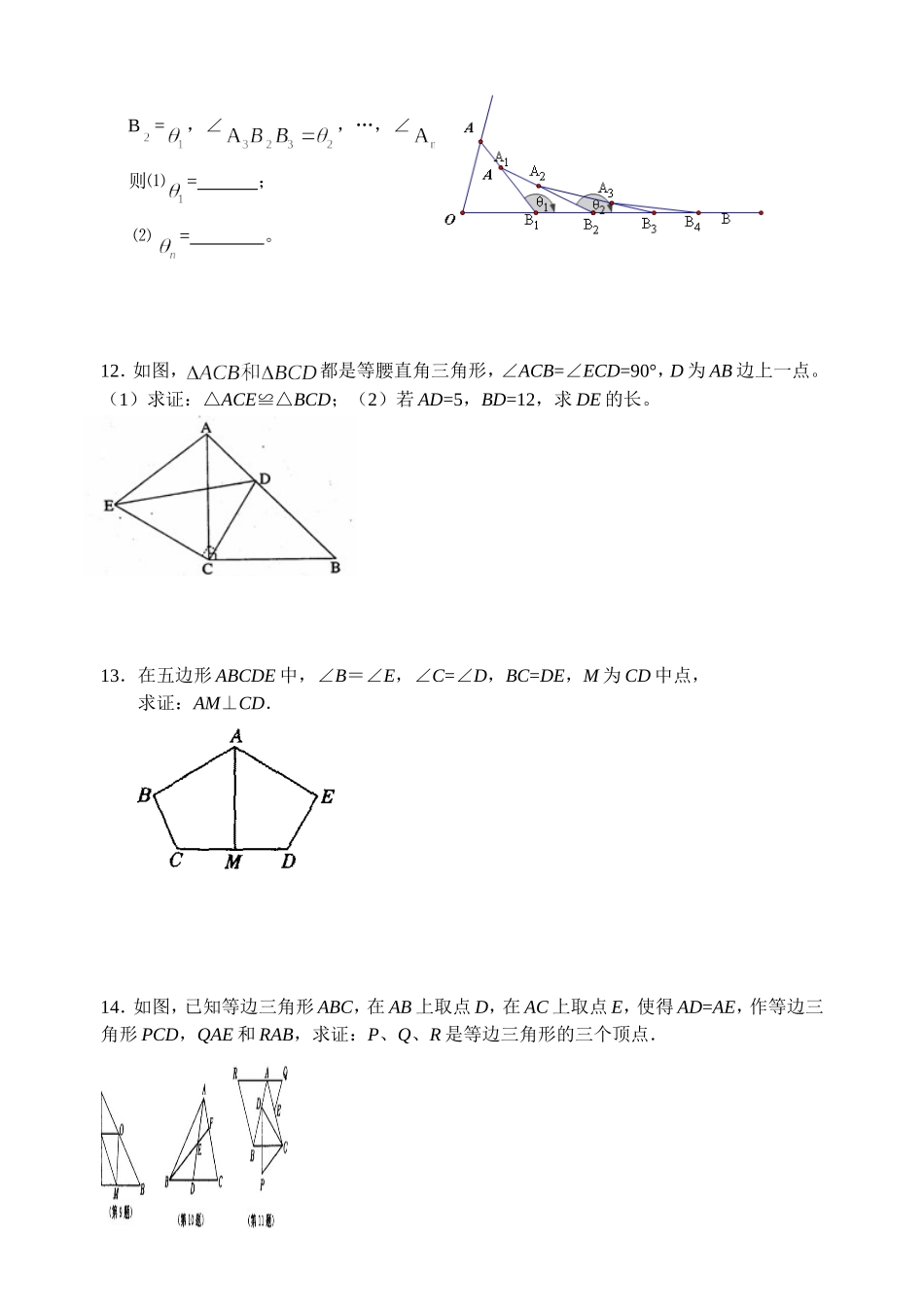
八年级数学练习4---等腰三角形1.如果一个等腰三角形中∠A=50o,则∠B=.2.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A=.3.如图,ABC△中,ABAC,AD⊥BC,若5cm6cmABBC,,则ADcm.4.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是.5.在等腰ABC△中,ABAC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为()A.7B.11C.7或11D.7或106.在△ABC中,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是.7.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为()A.130°B.120°C.110°D.100°8.如图,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠A=15°,求∠EDM=.9.如图,一个六边形的6个内角都是120°,其连续四边的长依次是1、9、9、5,那么这个六边形的周长是cm.10.在等边△ABC所在的平面内求一点P,使△PAB、△PBC、△PAC都是等腰三角形,具有这样性质的点P有()A.1个B.4个C.7个D.10个11.如图,已知∠AOB=,在射线OA、OB上分别取点OA=OB,连结AB,在BA、BB上分别取点A、B,使BB=BA,连结AB…按此规律上去,记∠ABl1l2l3ACBACDBABCDB=,∠,…,∠则⑴=;⑵=。12.如图,都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点。(1)求证:△ACE≌△BCD;(2)若AD=5,BD=12,求DE的长。13.在五边形ABCDE中,∠B=∠E,∠C=∠D,BC=DE,M为CD中点,求证:AM⊥CD.14.如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.15.著名的恩施大峡谷()A和世界级自然保护区星斗山()B位于笔直的沪渝高速公路X同侧,50kmABA,、B到直线X的距离分别为10km和40km,要在沪渝高速公路旁修建一服务区P,向A、B两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(AP与直线X垂直,垂足为P),P到A、B的距离之和1SPAPB,图(2)是方案二的示意图(点A关于直线X的对称点是A,连接BA交直线X于点P),P到A、B的距离之和2SPAPB.(1)求1S、2S,并比较它们的大小;(2)请你说明2SPAPB的值为最小;(3)拟建的恩施到张家界高速公路Y与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,B到直线Y的距离为30km,请你在X旁和Y旁各修建一服务区P、Q,使P、A、B、Q组成的四边形的周长最小.并求出这个最小值.16.如图,△ABC和△ADC都是每边长相等的等边三角形,点E、F同时分别从点B、A出发,各自沿BA、AD方向运动到点A、D停止,运动的速度相同,连接EC、FC.(1)在点E、F运动过程中∠ECF的大小是否随之变化?请说明理由;(2)在点E、F运动过程中,以点A、E、C、F为顶点的四边形的面积变化吗?请说明理由.(3)连接EF,在图中找出和∠ACE相等的所有角,并说明理由.(4)若点E、F在射线BA、射线AD上继续运动下去,(1)小题中的结论还成立吗?BAPX图(1)YXBAQPO图(3)BAPXA图(2)AEBCDF17.如图,已知ABC△中,10ABAC厘米,8BC厘米,点D为AB的中点.(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,经过1秒后,BPD△与CQP△是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使BPD△与CQP△全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿ABC△三边运动,求经过多长时间点P与点Q第一次在ABC△的哪条边上相遇?18.已知等腰直角△ABC,∠C=90°,AC=BC,D、E是AB边上的点,且∠DCE=45°,求证:AQCDBPEDCBA