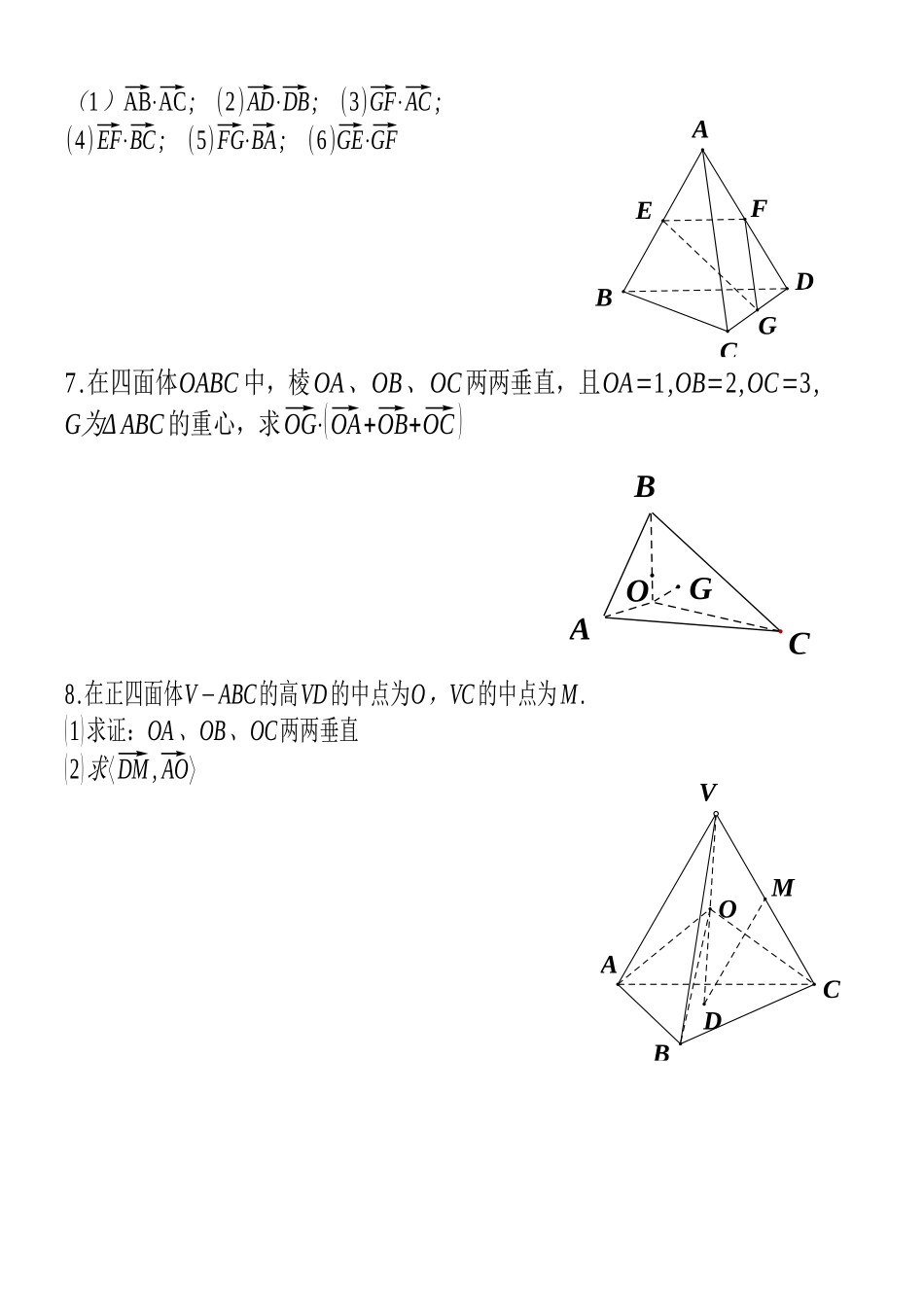
作业案1.已知空间四边形ABCD的每条边和对角线的长都等于a,E点,F分别是BC,AD的中点,则⃗AE⋅⃗AF的值为()A.¿a2¿B.¿12a2¿C.¿14a2¿D.¿√34a2¿2.已知四边形ABCD为矩形,PA⊥平面ABCD,连接的AC,BD,PB,PC,PD,则下列各组向量中,数量积不为0的是()A.¿⃗PC与⃗BD¿B.¿⃗DA与⃗PB¿C.¿⃗PD与⃗AB¿D.¿⃗PA与⃗CD¿3.正方体ABCD−A1B1C1D1的棱长为a,对角线AC1和BD1相交于点O,则有()A.¿⃗AB⋅⃗A1C1=2a2¿B.¿⃗AB⋅⃗AC1=√2a2¿C.¿⃗AO⋅⃗AB=12a2¿D.¿⃗BC⋅⃗DA1=a2¿4..在空间四边形OABC中,OB=OC,∠AOB=∠AOC=π3,则⟨⃗OA,⃗BC⟩=()A.¿12¿B.¿√22¿C.¿−12¿D.¿0¿5.在平行六面体ABCD−A'B'C'D'中,AB,AD,AA'两两夹角均为60∘,且AB=1,AD=2,AA'=3,则⃗AA'⋅⃗AC'=_________________B'D'C'A'ABDC6.已知四面体ABCD每条棱长都等于a,E点,F,G分别是棱AB,AD,DC的中点。求下列向量的内积:7.在四面体OABC中,棱OA、OB、OC两两垂直,且OA=1,OB=2,OC=3,GΔ为ABC的重心,求⃗OG⋅(⃗OA+⃗OB+⃗OC)8.在正四面体V−ABC的高VD的中点为O,VC的中点为M.(1)求证:OA、OB、OC两两垂直(2)求⟨⃗DM,⃗AO⟩GFEDABCGBCOAMODVABC(1)⃗AB⋅⃗AC;(2)⃗AD⋅⃗DB;(3)⃗GF⋅⃗AC;(4)⃗EF⋅⃗BC;(5)⃗FG⋅⃗BA;(6)⃗GE⋅⃗GF