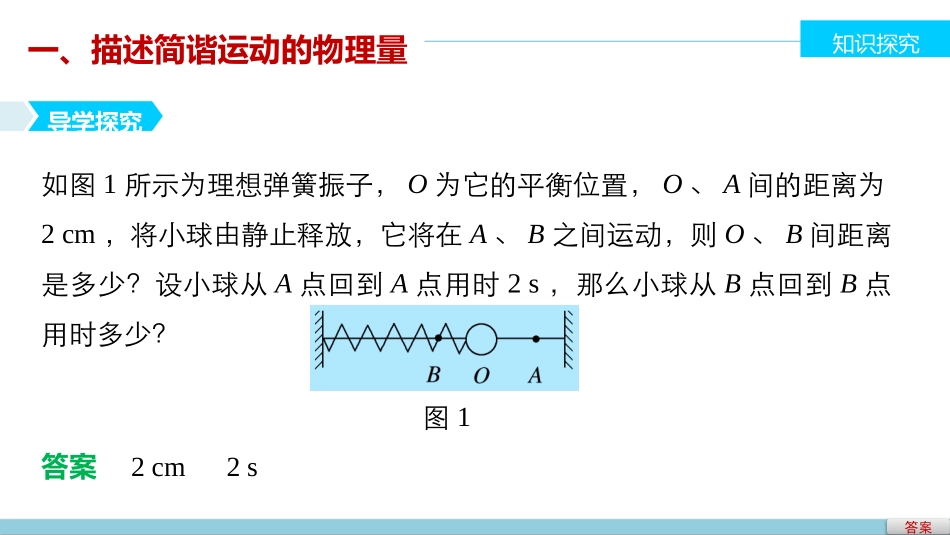
2简谐运动的描述第十一章机械振动学习目标知识探究典例精析达标检测1.知道什么是振动的振幅、周期、频率及相位.2.理解周期和频率的关系.3.知道简谐运动的数学表达式,知道其中各物理量的意义.一、描述简谐运动的物理量知识探究导学探究如图1所示为理想弹簧振子,O为它的平衡位置,O、A间的距离为2cm,将小球由静止释放,它将在A、B之间运动,则O、B间距离是多少?设小球从A点回到A点用时2s,那么小球从B点回到B点用时多少?图1答案2cm2s答案知识梳理描述简谐运动的物理量1.振幅:振动物体离开平衡位置的距离.2.全振动:振动物体往返一次(以后完全重复原来的运动)的运动叫做一次全振动.判断是否为全振动的方法:(1)如果物体的位移和都回到原值(大小、方向两方面),即物体从同一个方向回到出发点,则是一次全振动;(2)看物体通过的路程是否等于振幅的.3.周期和频率:(1)周期:振动物体完成全振动所需要的时间,最大速度四倍一次答案频率:单位时间内完成全振动的,T和f的关系为T=.(2)周期和频率由振动系统本身的性质决定,与振幅(填“有关”或“无关”).1f次数无关答案即学即用(多选)弹簧振子在AOB之间做简谐运动,O为平衡位置,测得A、B之间的距离为8cm,完成30次全振动所用时间为60s,则()A.振子的振动周期是2s,振幅是8cmB.振子的振动频率是2HzC.振子完成一次全振动通过的路程是16cmD.振子通过O点时开始计时,3s内通过的路为24cm解析答案二、简谐运动的表达式导学探究物体做简谐运动的位移随时间按正弦规律变化,可用正弦函数x=Asin(ωt+φ)描述简谐运动,则x、A、ω、φ、ωt+φ的意义各是怎样的?答案见知识梳理答案知识梳理对简谐运动表达式的理解简谐运动的表达式x=Asin(ωt+φ)反映了质点的位移随时间的变化关系,各量意义如下:(1)x表示振动物体相对于平衡位置的;t表示振动的.(2)A表示振动物体偏离平衡位置的最大距离,即.(3)ω称做简谐运动的,它也表示简谐运动振动的快慢,与周期T及频率f的关系:ω==.2πT位移时间振幅圆频率2πf答案(4)ωt+φ代表简谐运动的相位;其中φ是t=0时的相位,称为初相位或初相.相位是一个角度,单位是或.(5)相位差若两个简谐运动的表达式为x1=A1sin(ωt+φ1),x2=A2sin(ωt+φ2),则相位差为Δφ==.当Δφ=时,两振动物体振动步调一致.当Δφ=时,两振动物体振动步调完全相反.弧度度(ωt+φ2)-(ωt+φ1)φ2-φ10π答案即学即用两个简谐运动分别为x1=4asin(4πbt+12π)和x2=2asin(4πbt+32π),则它们的振幅之比为______,各自的频率f1=______,f2=______.解析由x=Asin(ωt+φ)可知:A1=4a,A2=2a,所以A1∶A2=2∶1;ω1=ω2=4πb,根据ω=2πf可得f1=f2=2b.2∶12b2b返回解析答案一、描述简谐运动的物理量及其关系典例精析例1弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间的距离是20cm,振子由A运动到B的时间是2s,如图2所示,则()图2A.从O→B→O振子做了一次全振动B.振动周期为2s,振幅是10cmC.从B开始经过6s,振子通过的路程是60cmD.从O开始经过3s,振子处在平衡位置解析答案规律总结二、对简谐运动表达式的理解例2一个小球和轻质弹簧组成的系统,按x1=5sin(8πt+π)cm的规律振动.(1)求该振动的周期、频率、振幅和初相;14解析已知ω=8πrad/s,由ω=2πT得T=14s,f=1T=4Hz.A=5cm,φ1=π4.答案14s4Hz5cmπ4解析答案(2)另一简谐运动表达式为x2=5sin(8πt+π)cm,求它们的相位差.54解析由Δφ=(ωt+φ2)-(ωt+φ1)=φ2-φ1得Δφ=54π-π4=π.答案π解析答案三、简谐运动的周期性和对称性例3一水平弹簧振子做简谐运动,周期为T,则()A.若t时刻和(t+Δt)时刻振子运动位移的大小相等、方向相同,则Δt一定等于T的整数倍B.若t时刻和(t+Δt)时刻振子运动位移的大小相等、方向相反,则Δt一定等于的整数倍C.若Δt=T,则在t时刻和(t+Δt)时刻振子振动的速度一定相等D.若Δt=,则在t时刻和(t+Δt)时刻弹簧的长度一定相等T2T2解析答案归纳总结针对训练如图4所示,一质点沿水平直线做简谐运动,先后以相同速度通过a、b两点,经历时间tab=1s,过b点后再经t′=1s质点第一次反向...