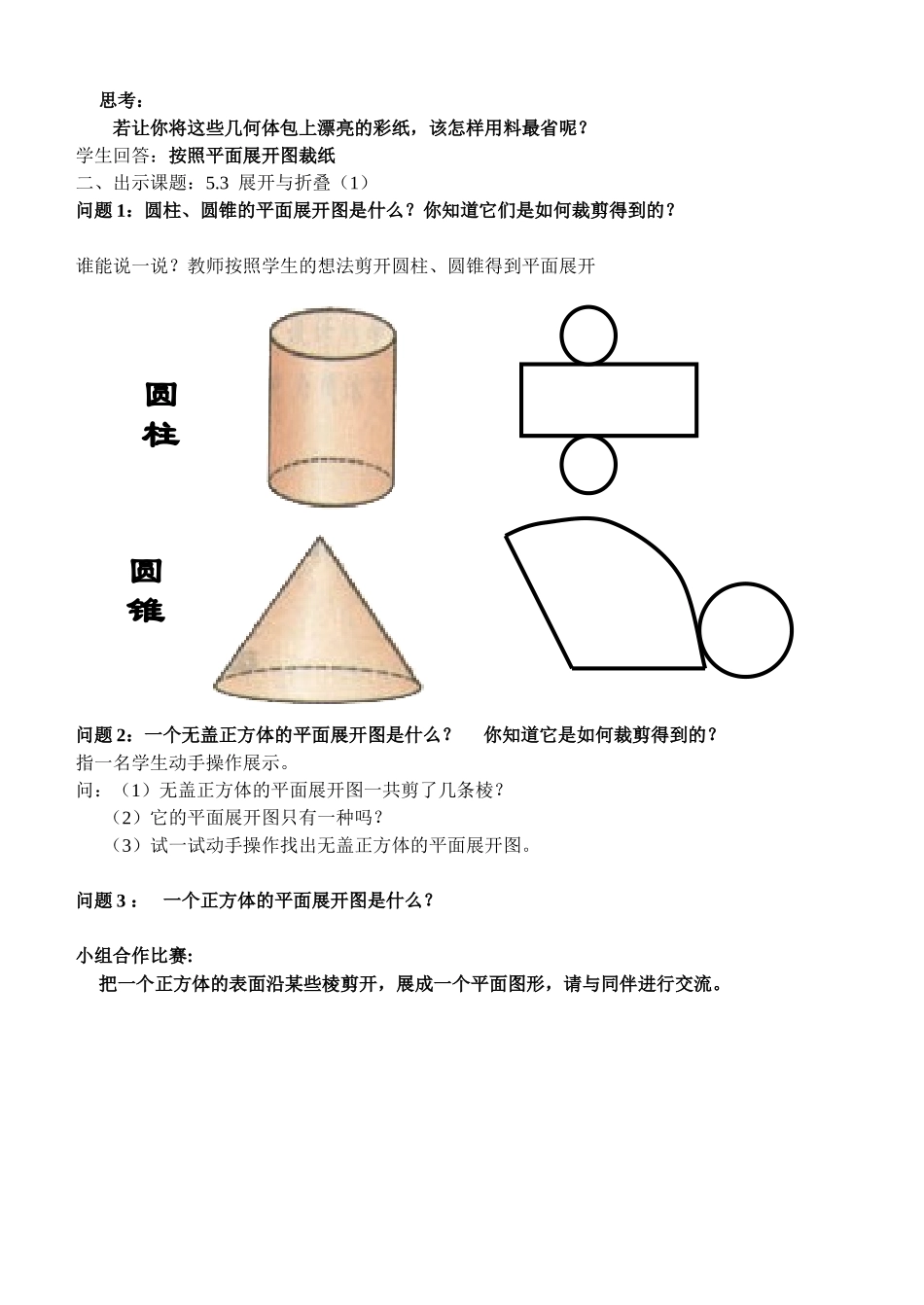
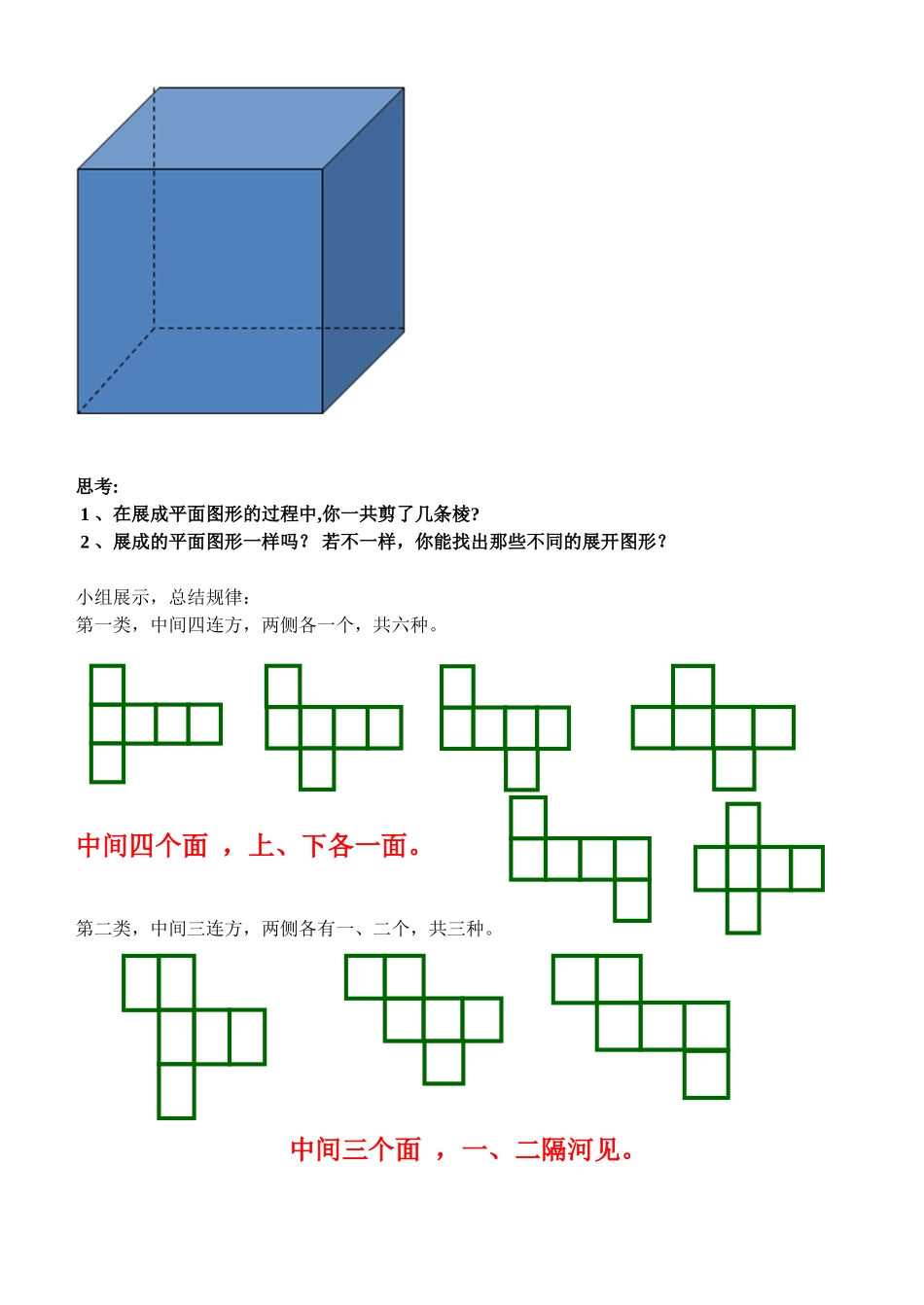
5.3展开与折叠(1)【教学目标】1.学生通过动手实验、展开讨论等方法,认识多面体与它们展开图的关系;2.让学生经历几何体的展开与折叠等实验活动,丰富空间观念,发展空间想象能力,养成研究性学习的良好习惯;3.获得研究问题的方法和经验;4.通过克服困难的经历和获得成功的体验,培养对数学的兴趣.【教学重点】1.通过正方体表面的展开与折叠活动,认识多面体与它们展开图的关系,积累数学活动的经验;2.丰富空间观念,发展空间想象能力.【教学难点】建立空间观念,想象几何体的展开与折叠过程.【教学准备】:教具准备:一个正方体纸盒、一个圆柱形纸筒、一个圆锥形纸筒、一把小剪刀。学具准备:每人两个块规定边长的正方、一个无盖正方体、小剪刀。【教学内容】一、出示图片思考:若让你将这些几何体包上漂亮的彩纸,该怎样用料最省呢?学生回答:按照平面展开图裁纸二、出示课题:5.3展开与折叠(1)问题1:圆柱、圆锥的平面展开图是什么?你知道它们是如何裁剪得到的?谁能说一说?教师按照学生的想法剪开圆柱、圆锥得到平面展开问题2:一个无盖正方体的平面展开图是什么?你知道它是如何裁剪得到的?指一名学生动手操作展示。问:(1)无盖正方体的平面展开图一共剪了几条棱?(2)它的平面展开图只有一种吗?(3)试一试动手操作找出无盖正方体的平面展开图。问题3:一个正方体的平面展开图是什么?小组合作比赛:把一个正方体的表面沿某些棱剪开,展成一个平面图形,请与同伴进行交流。圆锥圆柱思考:1、在展成平面图形的过程中,你一共剪了几条棱?2、展成的平面图形一样吗?若不一样,你能找出那些不同的展开图形?小组展示,总结规律:第一类,中间四连方,两侧各一个,共六种。中间四个面,上、下各一面。第二类,中间三连方,两侧各有一、二个,共三种。中间三个面,一、二隔河见。第三类,中间二连方,两侧各有二个,只有一种。中间两个面,楼梯天天见第四类,两排各三个,只有一种。中间没有面,三、三连一线下列哪些是正方体的展开图?难点突破:以下图形不是正方体的展开图(即无法折叠成正方体),请记住!三、小结,解决问题:一个正方体木块的2个相距最远的顶点处停了一只壁虎和一只蚊子,那么壁虎可以从哪条最短的路径爬到蚊子处?说明理由四、练习:1.一蚂蚁从圆柱上的A点出发,绕圆柱一圈到达B点,你能画出它爬行的最短路线吗?五、总结:1、学会了简单几何体(如三棱锥,正方体等)的平面展开图,知道按不同的式展开会得到不同的展开图。2、学会了动手实践,与同学合作。3、友情提醒:不是所有立体图形都有平面展开图,比如球体。六、作业:补充练习。七、板书设计:5.3展开与折叠(1)中间四个面,上、下各一面。中间三个面,一、二隔河见。中间两个面,楼梯天天见中间没有面,三、三连一线教学反思:1、大量的教学实践活动,展示了新课改,体现了教学活动过程中学生的主体作用。2、学生通过实物的展开操作活动,感受了数学来源于生活,数学应用于生活,并接受了实践是检验真知的标准。3、通过简单图形的折叠,学生接受了简单图形是复杂图形形成的基础,也增强了学生动手操作的能力。