中考第一轮复习-二次函数(1)如何求二次函数表达式VIP免费

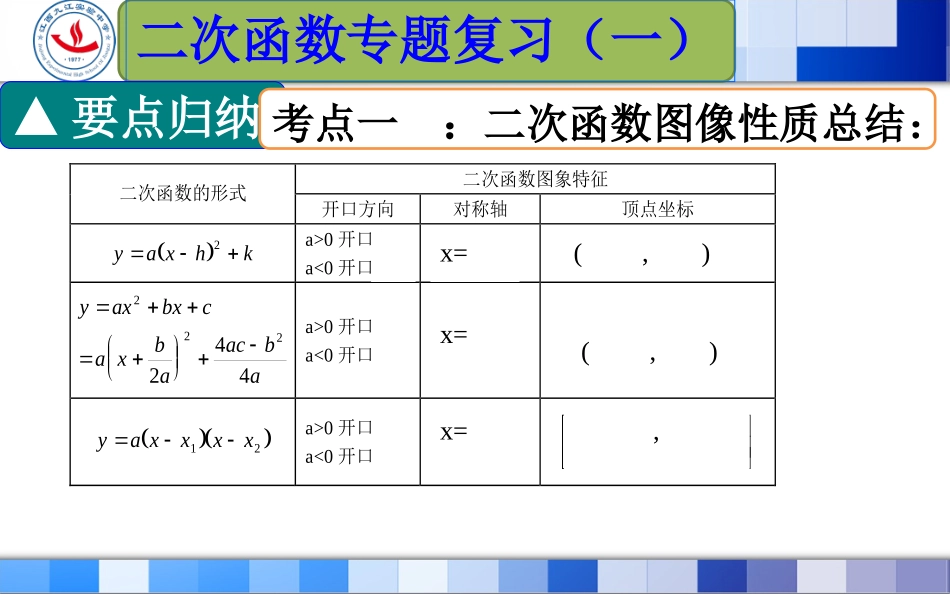
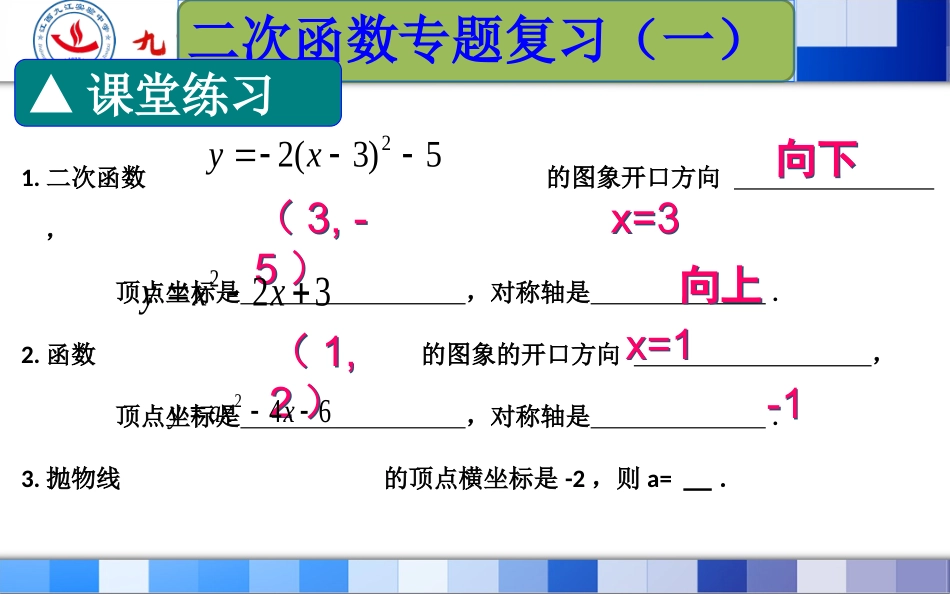
课程名称：如何求二次函数表达式课程名称：如何求二次函数表达式课程年级：中考第一轮复习课程年级：中考第一轮复习课程版本：北师大版课程版本：北师大版主讲教师：九江实验中学刘丽主讲教师：九江实验中学刘丽二次函数专题复习（一）▲要点归纳二次函数图象特征二次函数的形式开口方向对称轴顶点坐标yaxhk2a>0开口向上a<0开口向下xhhk，yaxbxcaxbaacba222244a>0开口向上a<0开口向下xba2baacba2442，yaxxxx12a>0开口向上a<0开口向下221xxx2212142xxaxx，(,)(,)x=x=x=,考点一：二次函数图像性质总结：1.二次函数的图象开口方向，顶点坐标是，对称轴是.2.函数的图象的开口方向，顶点坐标是，对称轴是.3.抛物线的顶点横坐标是-2，则a=．5)3(22xy向下向下（3,-5）（3,-5）x=3x=3二次函数专题复习（一）▲课堂练习322xxy向上向上（1,2）（1,2）x=1x=1642xaxy-1-14.函数，当x为时，函数有最大值，最大值是____.5.若将二次函数配方为y=的形式，则解析式为_________________.6.若抛物线y=x2-2x-3与x轴分别交于A、B两点，则AB的长为_________.322xxy2(1)2yx44二次函数专题复习（一）a(x-h)2+k▲课堂练习)32(xxy1313▲要点归纳考点二：用待定系数法求二次函数的表达式：名称表达式已知条件待定系数顶点式y=_______________(a≠0)顶点坐标，和另一个点坐标求出a还回表达式一般式y=_______________(a≠0)任意三个点坐标求出a，b，c还回表达式交点式y=________________a≠0)（不能作为最后结果）与x轴的两个点和另一个点求出a还回表达式再化为一般式a(x-h)2+kax2+bx+ca(x-x1)(x-x2)二次函数专题复习（一）【例1】已知抛物线y=ax2+bx+c经过点（1，0）（3,0）（0,6），求该抛物线的解析式.▲例题精讲二次函数专题复习（一）分析：观察这三个点的特殊性（1，0）和（3,0）是x轴上的点，（0,6）是y轴上的点（方法一）解：把（1，0）、（3,0）和（0,6）分别代入y=ax2+bx+c，得0=a+b+c0=9a+3b+cC=6a=2b=-8C=6∴y=2x2-8x+6(方法二)解：设y=a（x-1）（x-3），再代入（0,6），得二次函数专题复习（一）▲例题精讲【例2】如图，四边形ABCD是菱形，点D的坐标是(0，)，以点C为顶点的抛物线y＝ax2＋bx＋c恰好经过x轴上A，B两点．(1)求A，B，C三点的坐标；(2)求经过A，B，C三点的抛物线的解析式．3分析(1)：易证△AOD≌△BEC可得OA=EB,又由抛物线的对称性可知AE＝BE，设AD=2m，mmm2m3在Rt△AOD中，m2＋()2＝(2m)2，解得m＝13∴A(1,0)，B(3,0)，C(2，)3解(2)设抛物线的解析式为y＝a(x－2)2＋，代入A(1,0)，得a＝－.∴抛物线的解析式为y＝－(x－2)2＋.3333【例3】如图所示,一位篮球运动员在离篮圈水平距离为4m处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心离地面距离为3.05m.建立如图所示的直角坐标系,求抛物线所对应的函数关系式;▲例题精讲二次函数专题复习（一）分析：找出已知点①顶点（0,3.5）②另一点（1.5,3.05）应选用顶点式求解考点二：用待定系数法求二次函数的表达式：考点一：二次函数图像性质总结：考点三：二次函数的图像与系数a、b、c及b2-4ac的关系：▲课堂小结考点四：抛物线与几何图形的联系：二次函数专题复习谢谢大家！【例4】已知抛物线y=-x2+(6-)x+m-3与x轴有A、B两个交点,且A、B两点关于y轴对称(1)求m的值;(2)写出抛物线解析式及顶点坐标;2m解(1)设A(x1,0)B(x2,0).∵A、B两点关于y轴对称.∴解得m=6▲例题精讲二次函数专题复习（一）（2）抛物线解析式为y=-x2+3∴x1+x2=0且x1·x2>06-=0且m-3>02m顶点为（0,3）