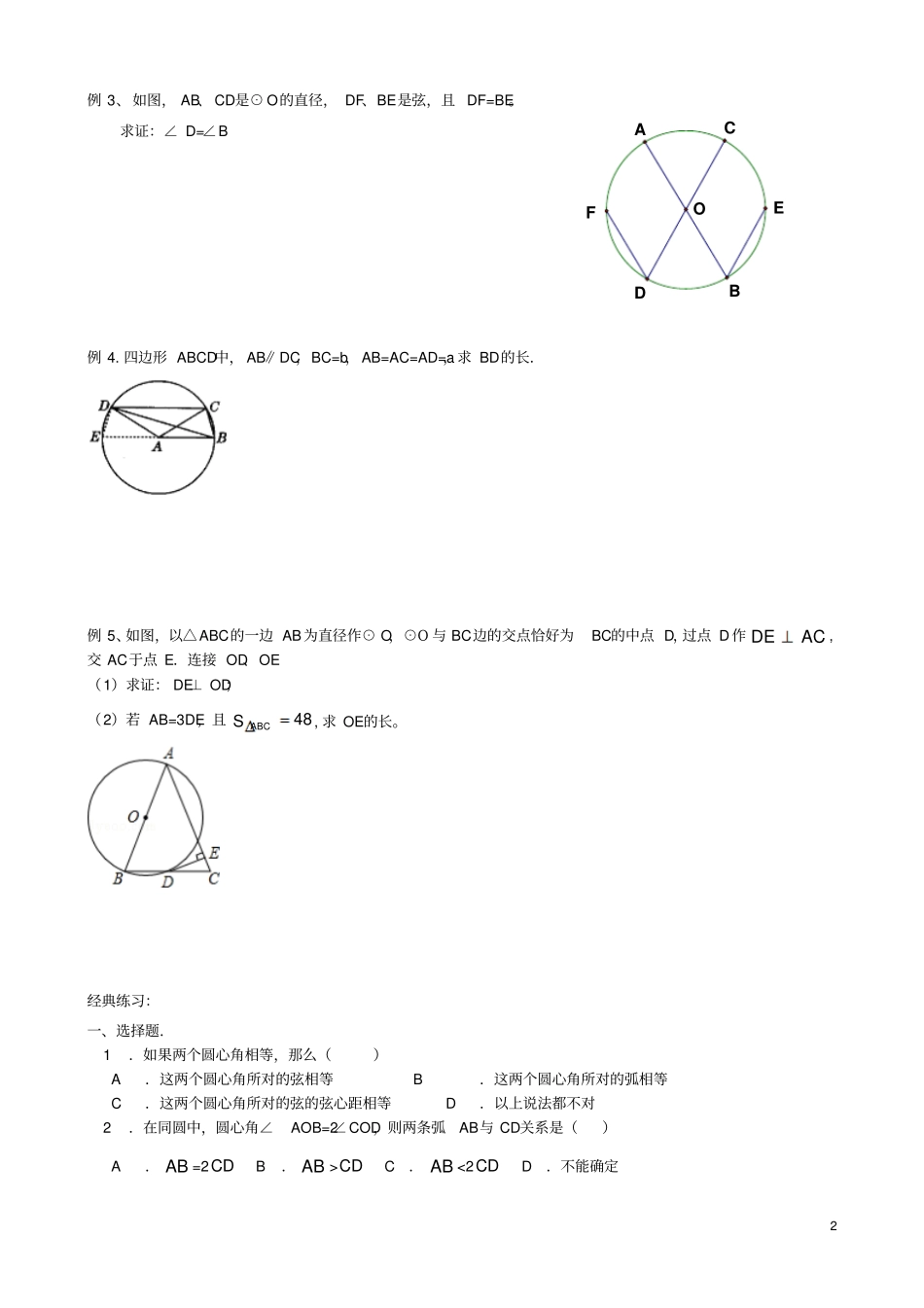
OABC圆知识要点梳理:一、圆心角的定义:如图所示,∠AOB的顶点在圆心,像这样顶点在圆心的角叫做圆心角.(∠AOB是AB所对的圆心角)二、圆心角定理及推论:(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等(2)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.(3)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.三、圆周角的定义:如图所示,∠ACB的顶点在圆周上,像这样的角叫做圆周角(∠ACB是AB所对的圆周角).四、圆周角的定理及推论:(1)定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,?都等于这条弧所对的圆心角的一半.(2)推论:半圆(或直径)所对的圆周角是直角,90?°的圆周角所对的弦是直径.五、圆的内接四边形对角互补,对角互补的四边形是圆的内接四边形经典例题:例1.如图,AB是⊙O的直径,∠DCB=30°,则∠ACD=°,∠ABD=°例2、如图,OA、OB、OC都是圆O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BACODCBA2CAEFDOB例3、如图,AB、CD是⊙O的直径,DF、BE是弦,且DF=BE。求证:∠D=∠B例4.四边形ABCD中,AB∥DC,BC=b,AB=AC=AD=a,求BD的长.例5、如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作ACDE,交AC于点E.连接OD、OE(1)求证:DE⊥OD;(2)若AB=3DE,且48ABCS,求OE的长。经典练习:一、选择题.1.如果两个圆心角相等,那么()A.这两个圆心角所对的弦相等B.这两个圆心角所对的弧相等C.这两个圆心角所对的弦的弦心距相等D.以上说法都不对2.在同圆中,圆心角∠AOB=2∠COD,则两条弧AB与CD关系是()A.AB=2CDB.AB>CDC.AB<2CDD.不能确定33.如图5,⊙O中,如果AB=2AC,那么().A.AB=ACB.AB=2ACC.AB<2ACD.AB>2ACOBAC(5)4.如图1,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于().A.140°B.110°C.120°D.130°OBACwww.czsx.com.cn2143OBACD(1)(2)(3)5.如图2,∠1、∠2、∠3、∠4的大小关系是()A.∠4<∠1<∠2<∠3B.∠4<∠1=∠3<∠2C.∠4<∠1<∠3<∠2D.∠4<∠1<∠3=∠26.如图3,AD是⊙O的直径,AC是弦,OB⊥AD,若OB=5,且∠CAD=30°,则BC等于().A.3B.3+3C.5-123D.5二、填空题1.一条弦长恰好为半径长,则此弦所对的弧是半圆的_________.2.如图6,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=________.3.若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于4.如图4,A、B是⊙O的直径,C、D、E都是圆上的点,则∠1+∠2=_______.?OBAC21EDOBACwww.czsx.com.cnOBACED(4)(5)(6)5.如图5,已知△ABC为⊙O内接三角形,BC=?1,∠A=?60°,则⊙O?半径为_______.4OBACDwww.czsx.com.cnOBACP三、解答题1.如图,在⊙O中,C、D是直径AB上两点,且AC=BD,MC⊥AB,ND⊥AB,M、N在⊙O上.(1)求证:AM=BN;(2)若C、D分别为OA、OB中点,则AMMNNB成立吗?OBACDwww.czsx.com.cnNM2.如图,以ABCD的顶点A为圆心,AB为半径作圆,分别交BC、AD于E、F,若∠D=65°,求BE的度数和EF的度数.BACEDwww.czsx.com.cnF3.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?4.如图,已知AB=AC,∠APC=60°(1)求证:△ABC是等边三角形.(2)若BC=4cm,求⊙O的面积.5HGIOEDABCF30°BANOMPOBACyxM5.如图,⊙C经过坐标原点,且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.(1)求证:AB为⊙C直径.(2)求⊙C的半径及圆心C的坐标.能力拓展1.如图所示,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点,点P是直径MN上一动点,则PA+PB的最小值是()A.2B.1C.2D.222.已知在菱形ABCD中,对角线AC、BD交于点E,F为BA延长线上一点,连接EF,以EF为直径的⊙O经过点D,与CD边交于点G.(1)求∠FDE;(2)判断四边形ACDF是什么四边形,说明理由(3)若G为CD中点,①求证:FD=FI②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.6ODBAC课后巩固:1.如图所示,A、B、C三点在圆O上,∠AOC=100°,则∠ABC等于()A.140°B.11...