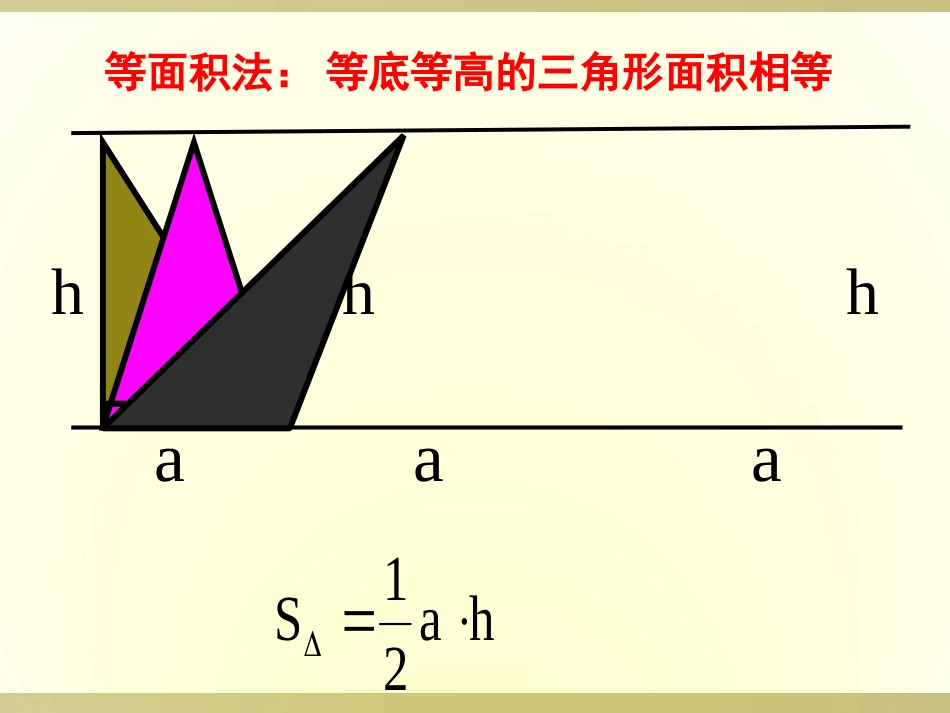
柱、锥、台和球体的体积复习回顾1.正方体的体积公式V正方体=a3(这里a为棱长)2.长方体的体积公式V长方体=abc(这里a,b,c分别为长方体长、宽、高)或V长方体=sh(s,h分别表示长方体的底面积和高)正方体的棱长为2,求它的体积长方体的长为3,宽为4,高为5,求它的体积。ha21Sahahah等底等高的三角形面积相等等面积法:取一摞作业本放在桌面上取一摞作业本放在桌面上((如图所如图所示示)),并改变它们的放置方法,观察改,并改变它们的放置方法,观察改变前后的体积是否发生变化?变前后的体积是否发生变化?从以上事实中你得到什么启发?从以上事实中你得到什么启发?一一..祖暅原理祖暅原理祖暅原理:幂势既同,则积不容异祖暅原理:幂势既同,则积不容异..也就是说,夹在也就是说,夹在两个平行平面两个平行平面间的间的两个几何体,被平行于这两个平面的两个几何体,被平行于这两个平面的任意任意平面平面所截,如果截得的两个截面的所截,如果截得的两个截面的面积总面积总相等相等,那么这两个几何体的,那么这两个几何体的体积相等体积相等..祖暅原理是推导柱、锥、台和球体祖暅原理是推导柱、锥、台和球体积公式的积公式的基础和纽带基础和纽带,原理中含有三个条,原理中含有三个条件,件,条件一是两个几何体夹在条件一是两个几何体夹在两个平行两个平行平面平面之间;之间;条件二是用条件二是用平行于两个平行平面平行于两个平行平面的的任何一平面可截得两个平面;任何一平面可截得两个平面;条件三是两个条件三是两个截面的面积总相等截面的面积总相等,,这三个条件缺一不可,否则结论不成立这三个条件缺一不可,否则结论不成立..祖冲之(公元429年─公元500年)是我国杰出的数学家,科学家。南北朝时期人,汉族人,字文远。生于宋文帝元嘉六年,卒于齐昏侯永元二年。其主要贡献在数学、天文历法和机械三方面。祖暅,祖冲之之子,圆满解决了球面积的计算问题,得到正确的体积公式。祖暅总结了刘徽的有关工作,提出“幂势既同则积不容异”,即等高的两立体,若其任意高处的水平截面积相等,则这两立体体积相等,这就是著名的“祖暅原理”(或刘祖原理)。祖暅应用这个原理,解决了刘徽尚未解决的球体积公式。该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年。祖暅的儿子祖皓,续传家学,后来也成了数学家。等底面积、等高的两个柱体是否体积相等?体积相等等高、等截面面积(不受截面形状影响)二二..棱柱和圆柱的体积棱柱和圆柱的体积柱体(棱柱和圆柱)的体积等于它的柱体(棱柱和圆柱)的体积等于它的底面底面积积SS和高和高hh的积的积..即即VV柱体柱体==SS··hh..hhhh底面半径是底面半径是RR,高为的圆柱体的体积的计,高为的圆柱体的体积的计算公式是算公式是VV圆柱圆柱=π=πRR22hh..三.锥体体积ABCC1A1B1以三棱柱为例B1A1ABCC1B1A1ABCC1B1A1C1CBA2.锥体体积1=3VSh锥体底面积为S,高为h的三棱锥的体积为B1A1C1CBA三三..棱锥和圆锥的体积棱锥和圆锥的体积1.1.如果一个锥体(棱锥、圆锥)的底面积如果一个锥体(棱锥、圆锥)的底面积是是SS,高是,高是hh,那么它的体积是,那么它的体积是VV锥体锥体==ShSh..312.2.如果圆锥的底面半径是如果圆锥的底面半径是RR,高是,高是hh,则,则它的体积是它的体积是VV圆锥圆锥=π=πRR22hh..31PS'hSO'OD'DABCA'B'C'四四..棱台和圆台的体积棱台和圆台的体积1.1.VV台体台体==;其中;其中SS、、SS’’分别为台体上、下底面面积,分别为台体上、下底面面积,hh为台体的为台体的高高..1('')3SSSShV柱体=sh)''(3sssshV台shV31锥S=S/S/=0SS’SS数形五五..球的体积球的体积VV球球==,其中,其中RR为球的半径为球的半径..343R例例1.1.如图所示,在长方体如图所示,在长方体ABCDABCD--AA’’BB’’CC’’DD’’中,用截面截下一个棱锥中,用截面截下一个棱锥CC--AA’’DDDD’’,求棱锥,求棱锥CC--AA’’DDDD’’的体积与剩余部的体积与剩余部分的体积之比。分的体积之比。D'DABCA'B'C'ADCBC/D/B/A/CA/D/DSh例例1.1.如图所示,在长方体如图所示,在长方体ABCDABCD--AA’’B...