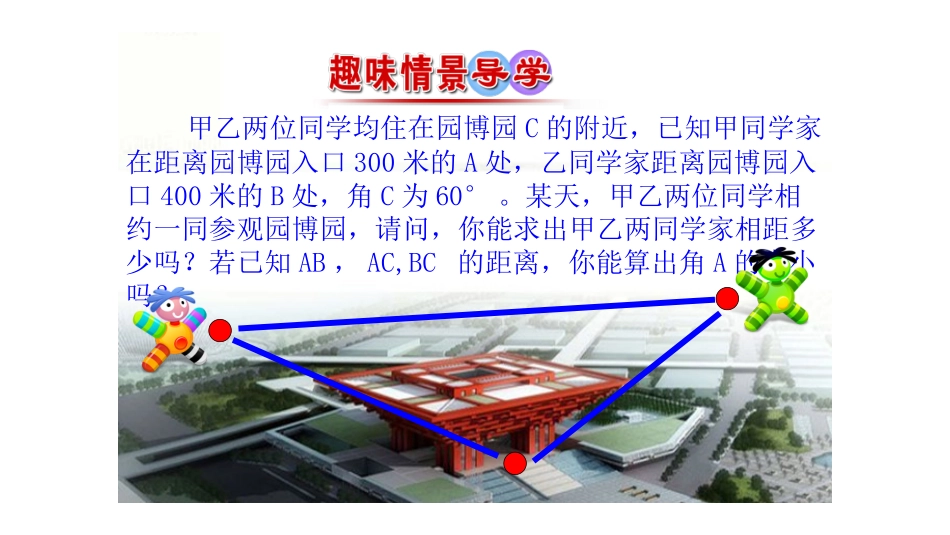
余弦定理的证明作者:刘成单位:丹江口市第一中学①已知三角形两边和一条边所对的角解三角形;正弦定理在解三角形中有两个应用,你知道吗?②已知三角形两角和一条边解三角形;温故甲乙两位同学均住在园博园C的附近,已知甲同学家在距离园博园入口300米的A处,乙同学家距离园博园入口400米的B处,角C为60°。某天,甲乙两位同学相约一同参观园博园,请问,你能求出甲乙两同学家相距多少吗?若已知AB,AC,BC的距离,你能算出角A的大小吗?①已知三角形两边和它们的夹角解三角形;另外两类解三角形问题②已知三角形三边解三角形;知新向量法证明:用正弦定理试求,发现因A、B均未知,所以较难求边c.由于涉及边长,从而可以考虑用向量来研究这个问题.如图,在△ABC中,设BC=a,AC=b,AB=c.已知a,b和C,求边c.提示:余弦定理证明2222222222cos2cos即c=ababcosC同理可得a=bcbcAb=acacB+-2几何法证明:①当△ABC为锐角三角形时,如下所示:作CD⊥AB,D为垂足,则CD=bsinA,DB=c-bcosA,则a2=DB2+CD2=(c-bcosA)2+(bsinA)2=b2+c2-2bccosA,其余两个式子同理可证;作CD⊥AB,交BA的延长线于点D,则CD=bsinA,DB=bcos(π-A)+c=c-bcosA,则a2=DB2+CD2=(c-bcosA)2+(bsinA)2=b2+c2-2bccosA,其余两个式子同理可证;③当△ABC为直角三角形时,利用勾股定理即可证明.②当△ABC为钝角三角形时,如图:三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍余弦定理用途:由余弦定理可知,已知三角形两边及其夹角可以求出三角形的第三条边.222222222abc2bccosAbac2accosBcab2abcosC.;;余弦定理的推论:用途:通过上述推论可知,由三角形的三条边可以求出三角形任意一角的余弦值.222222222cos2cos2bcaA=bcacbB=acabccosC=ab+-2222222222abc2bccosAbac2accosBcab2abcosC.;;你能推出cosA,cosB,cosC吗?思考:勾股定理指出了直角三角形中三边平方之间的关系,余弦定理则指出了一般三角形中三边平方之间的关系,你如何理解这两个定理之间的关系?由此可知余弦定理是勾股定理的推广,勾股定理是余弦定理的特例.22222cos900.,则=,这若在ABC中,C=90c=ababcosC=ab时+-2+提示:余弦定理与勾股定理的关系三、例题剖析【例1】在△ABC中,已知b=2,c=3,A=60°,则a=().【例2】已知在△ABC中,a=2,b=4,c=5,则cosA=________.【例3】在△ABC中,已知a=,b=,A=45°,求C及S△ABC.(两种方法)23课堂练习在△ABC中:(1)已知c=8,b=3,B=60°,求a;(2)已知a=9,b=10,c=15,求cosB;(3)已知a=33,c=2,B=150°,求b;①;几何法②向量法;一、余弦定理的两种证明方法总结二、余弦定理在解三角形中的两个应用①已知三角形两边和它们的的夹角解三角形;三、余弦定理与勾股定理的关系余弦定理是勾股定理的推广,勾股定理是余弦定理的特例②已知三角形三条边解三角形;