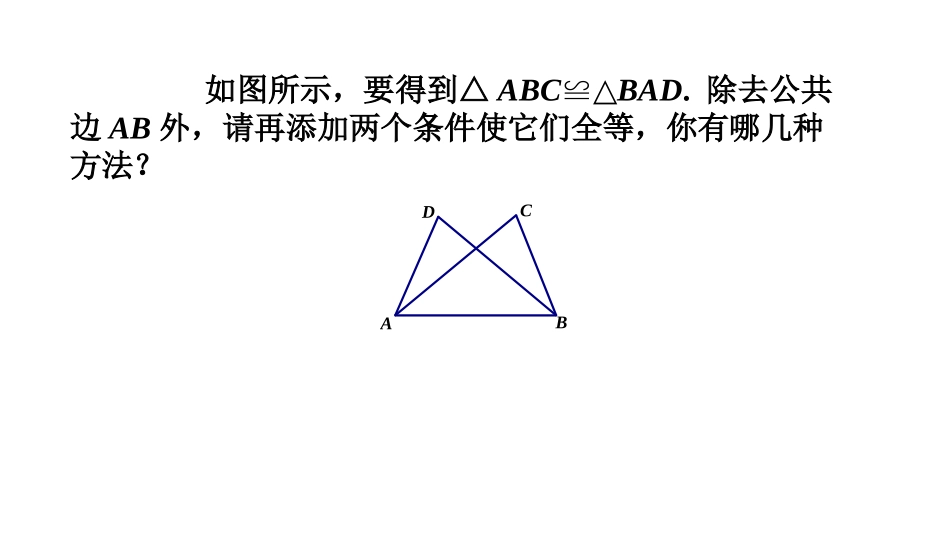
第二部分专题探究深度学习第五讲三角形相关知识复习——以三角形旋转为基架的几何题目探讨2017.5.10如图所示,要得到△ABC≌△BAD.除去公共边AB外,请再添加两个条件使它们全等,你有哪几种方法?ABCD如图所示,要得到△ABC≌△BAD.除去公共边AB外,请再添加两个条件使它们全等,你有哪几种方法?(1)AC=BD,BC=AD(SSS)(2)AC=BD,∠CAB=∠DBA(SAS)(3)BC=AD,∠C=∠D(SAS)(4)∠CAB=∠DBA,∠CBA=∠DAB(ASA)(5)∠CAB=∠DBA,∠C=∠D(AAS)(6)∠CBA=∠DAB,∠C=∠D(AAS)(7)∠C=∠D=90°,BC=AD(HL)(8)∠C=∠D=90°,AC=BD(HL)ABCD如图,在△ABC中,AE⊥BC于E,AE=BE,D是AE上一点,且DE=CE,试判断BD与AC有何关系?并说明理由.例:BCAED如图,在△ABC中,AE⊥BC于E,AE=BE,D是AE上一点,且DE=CE,试判断BD与AC有何关系?并说明理由.例:解:BD=AC且BDAC.⊥理由如下: AEBC⊥于E,∴∠BED=AEC=90°.∠在△BDE和△ACE中,AE=BE,∠BED=AEC∠,DE=CE,∴△BDE≌△ACE.(SAS)∴BD=AC.延长BD与AC交于点F,由△BDE≌△ACE可得,∠DBE=CAE∠,而∠BDE=ADF∠,∴∠BFC=ADF+DAF=BDE+DBE=90°∠∠∠∠∴BD=AC且BDAC.⊥BCAEDF如图,连接CD,得到等腰直角△ABE和等腰直角△CDE,将△CDE绕点E转动,请问BD与AC的关系是否会改变?并说明理由.变式:DBEACDBEACDBEAC将△CDE绕点E转动的过程中,直线BD与直线AC交点运动的轨迹是什么?请说明理由.变式:DBEACDBEACDBEAC如果将△CDE的直角边进行放大或缩小后绕点E转动,直线BD与直线AC交点运动的轨迹是否会改变?请说明理由.变式:DBEACKDBEACKDBEAC课堂小结:DBEACKDBEACKDBEACDBEACDBEAC到底是什么决定了刚才一系列变化过程中的变与不变?课堂小结:DBEACKDBEACKDBEACDBEACDBEAC将复杂的图形进行分解和转化找基本图形,找基本变化.在变化中找出不变可以帮助我们较好的解决复杂问题.在刚才的所有旋转变化中,我们始终找到了变化中的不变,之所以不变,是由于△ABE与△CDE的形状和大小没有发生变化,如果改变它们边或角的条件,能否得出新的结论呢?变式:DBEACDBEACDBEAC变式中考:1.(2016年成都中考)如图①,△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,DH=CH,连接BD.(1)求证:BD=AC;(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应).连接AE.ⅰ)如图②,当点F落在AC上时(F不与C重合).设BC=4,tanC=3,求AE的长;ⅱ)如图③,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接GH.试探究线段GH与EF之间满足的等量关系,并说明理由.图①图②图③1.(2016年成都中考)如图①,△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,DH=CH,连接BD.(1)求证:BD=AC;(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应).连接AE.ⅰ)如图②,当点F落在AC上时(F不与C重合).设BC=4,tanC=3,求AE的长;ⅱ)如图③,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接GH.试探究线段GH与EF之间满足的等量关系,并说明理由.图①图②图③1.(2016年成都中考)如图①,△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,DH=CH,连接BD.(1)求证:BD=AC;(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应).连接AE.ⅰ)如图②,当点F落在AC上时(F不与C重合).设BC=4,tanC=3,求AE的长;ⅱ)如图③,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接GH.试探究线段GH与EF之间满足的等量关系,并说明理由.图①图②图③DBEDBCHCHAAF变式中考:4.(2012年成都中考)如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=92a时,P,Q两点间的距离(用含a的代数式表示).QP图①FEDCBAABCDEF图②PQ2.变式中考:2.(2015年成都中考)已知AC...