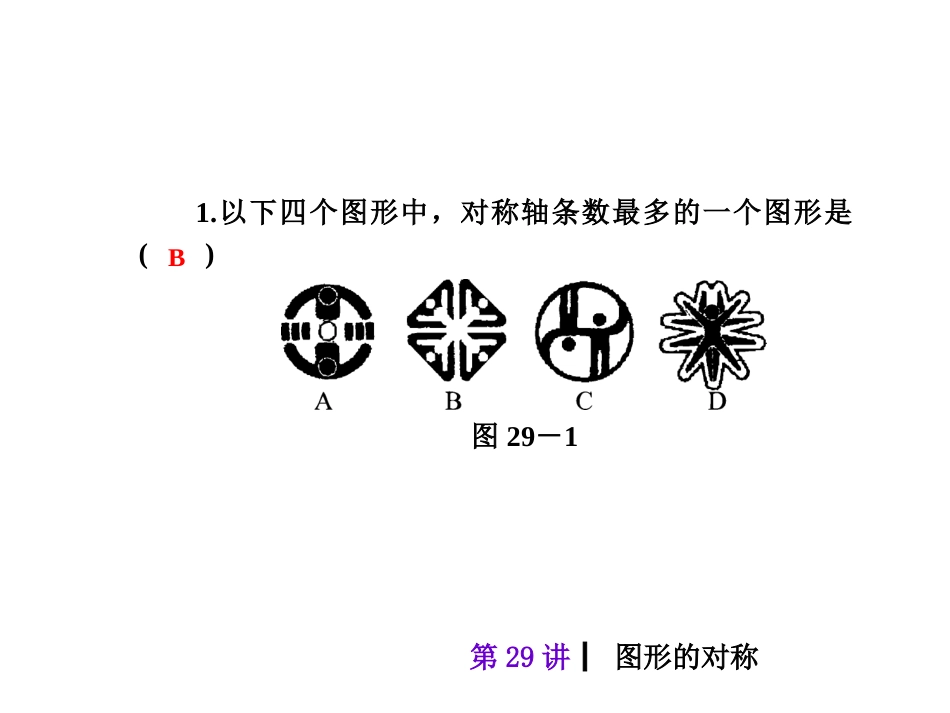
考点1轴对称及其性质┃考点自主梳理与热身反馈┃第29讲┃图形的对称轴对称把一个图形沿着某一条直线折叠,能够与另一个图形_______,这两个图形关于这条直线对称,这条直线就是_________轴对称图形把一个图形沿某一条直线折叠,直线两旁的部分能够_______,这个图形叫做轴对称图形,这条直线是_________性质①对称轴是任何一对对应点所连线段的_______;②对应角_______,对应线段______区别轴对称是指两个图形能够重合,而轴对称图形是对一个图形而言相等重合对称轴重合对称轴垂直平分线相等第29讲┃图形的对称1.以下四个图形中,对称轴条数最多的一个图形是()图29-1B第29讲┃图形的对称2.如图29-2是一辆汽车车牌在水中的倒影,则该车的牌照号码是()图29-2A.W17639B.W17936C.M17639D.M17936D第29讲┃图形的对称3.如图29-3所示,把一个正方形对折两次后沿虚线剪下,展开后所得的图形是()图29-3图29-4[解析]解题关键是明确两条折痕都是对称轴,故本题可借助空间想象,将两次对折后的图形沿两条折痕展开,易知展开后的图形应是B.B第29讲┃图形的对称4.如图29-5,△ABC和△A′B′C′关于直线l对称,下列结论中:①△ABC≌△A′B′C′;②∠BAC′=∠B′AC;③l垂直平分CC′;④直线BC和B′C′的交点不一定在l上.正确的有()图29-5A.4个B.3个C.2个D.1个B第29讲┃图形的对称5.在由四个相同的小正方形组成的“7”字形图中,请你添画一个小正方形,使它成为轴对称图形,并用虚线画出所得轴对称图形的对称轴.要求在图中画出三种不同的设计方案.图29-6点(a,b)关于直线x=m对称的点的坐标为(2m-a,b);点(a,b)关于直线y=n对称的点的坐标为(a,2n-b)(1)角是轴对称图形,它的对称轴是_____;(2)线段是轴对称图形,它的对称轴是_____;(3)圆是轴对称图形,它的对称轴是_____.1.等腰三角形的概念定义:有两边相等的三角形叫做等腰三角形,其中相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰与底边的夹角叫做底角.2.等腰三角形的性质性质:(1)等腰三角形的两个底角相等(简称为“等边对等角”);(2)等腰三角形的顶角平分线、底边上的高线、底边上的中线(简称为“三线合一”).3.等腰三角形的判定判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称为“等角对等边”).注意:要正确区别等腰三角形的性质和判定.“性质”指的是由边相等得出角相等,即“等边对等角”;而“判定”指的是根据一些条件来判定三角形是不是等腰三角形,即最后得出边相等.4.等边三角形定义:三边都相等的三角形叫做等边三角形.注意:等边三角形是等腰三角形的特殊情况,它是底边与腰相等的等腰三角形.5.等边三角形的性质和判定性质:(1)等边三角形的三条边都;(2)等边三角形的每一个角都等于.判定:(1)各边或角都相等的三角形是等边三角形;(2)有一个角等于的等腰三角形是等边三角形.相关规律:(1)边长为a的等边三角形面积等于;(2)等边三角形的内心、外心、垂心和重心重合于一点.60°相等60°6.线段的垂直平分线定义:经过线段的与这条线段的直线叫做这条线段的垂直平分线.注意:线段的垂直平分线的两个要点“垂直”和“平分”要同时存在.性质:线段垂直平分线上的点与这条线段两个端点的距离.判定:与一条线段两个端点距离的点,在这条线段的垂直平分线上.中点垂直相等相等图27-4,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得锐角为50°,则∠B=.如图,正方形ABCD中,AB=4,E是BC的中点,点P是对角线AC上一动点,则PE+PB的最小值为________.如图,已知点A是锐角∠MON内任意一点,试分别在OM、ON上确定点B、点C,使△ABC的周长最小.写出你作图的主要步骤并标明你所确定的点.(要求画出草图,保留作图痕迹)归类探究类型之一等腰三角形的性质的运用如图27-1,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为如图,已知正方形ABCD的对角线长为22,将正方形ABCD沿直线EF折叠,则图...