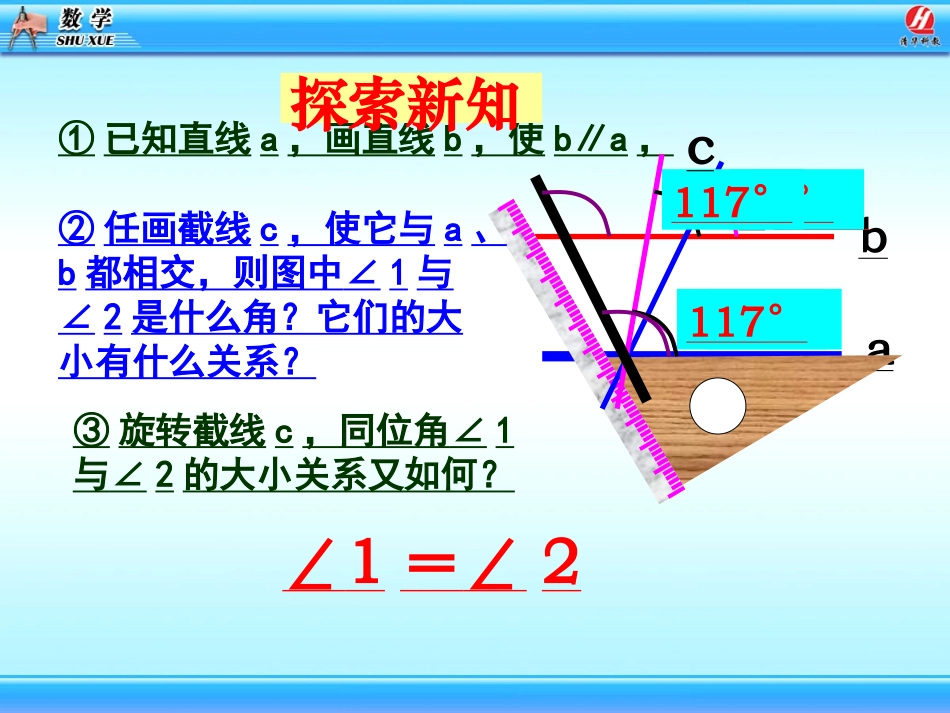
同位角相等,两直线平行。内错角相等,两直线平行。同旁内角互补,两直线平行。平行线的判定定理:两直线平行,同位角相等两直线平行,内错角相等两直线平行,同旁内角补反过来:是否正确呢?①已知直线a,画直线b,使b∥a,ab②任画截线c,使它与a、b都相交,则图中∠1与∠2是什么角?它们的大小有什么关系?1258°58°82°82°117°117°③旋转截线c,同位角∠1与∠2的大小关系又如何?∠1=∠2c探索新知65°65°cab12合作交流一合作交流一b2ac1∠∠1=2∠1=2∠两直线平行,同位角相等.平行线的性质平行线的性质11结论结论两条平行线被第三条直线所截,同位角相等.性质发现性质发现∴∴∠∠1=2.∠1=2.∠ ab,∥简写为:符号语言:b12ac如图:已知a//b,那么2与3相等吗?为什么?解 ab(∥已知),∴∠1=2(∠两直线平行,同位角相等).又 ∠1=3(∠对顶角相等),∴∠2=3(∠等量代换).合作交流二合作交流二b12ac3两直线平行,内错角相等.平行线的性质平行线的性质22结论结论两条平行线被第三条直线所截,内错角相等.性质发现性质发现∴∴∠∠2=3.∠2=3.∠ ab,∥符号语言:简写为:b12ac3解: a//b(已知),如图,已知a//b,那么2与4有什么关系呢?为什么?合作交流三合作交流三b12ac4∴1=2(两直线平行,同位角相等). 1+4=180°(邻补角定义),∴2+4=180°(等量代换).两直线平行,同旁内角互补.平行线的性质平行线的性质33结论结论两条平行线被第三条直线所截,同旁内角互补.性质发现性质发现∴∴2+4=180°. ab,∥符号语言:简写为:b12ac4性质1:两直线平行,同位角相等.性质2:两直线平行,内错角相等.性质3:两直线平行,同旁内角互补.平行线的性质:ab1234得出结论例如图,已知直线ab∥,∠1=500,求∠2的度数.abc12∴∠2=500(等量代换).解: ab(∥已知),∴∠1=2∠(两直线平行,内错角相等).又 ∠1=500(已知),变式1:已知条件不变,求∠3,∠4的度数?34师生互动师生互动,,典例示范典例示范变式2:已知∠3=∠4,∠1=47°,求∠2的度数?∴∠2=470()解: ∠∠3=4(∠3=4(∠))∴ab∥()又 ∠1=470()c1234abd如图在四边形ABCD中,已知AB∥CD,∠B=600.①求∠C的度数;②由已知条件能否求得∠A的度数?ABCD解:ABCD(① ∥已知),∴∠B+C=180∠0(两直线平行,同旁内角互补).又 ∠B=600(已知),∴∠C=1800-B∠=1800-600=1200(等式的性质).②根据题目的已知条件根据题目的已知条件,,无法求出无法求出∠A的度数的度数..BCAD解 AB∥CD(已知)∴∠B=∠C(两直线平行,内错角相等)又 ∠B=142°∴∠C=∠B=142°(已知)(等量代换)练习、一自行车运动员在一条公路上骑车,两次拐弯后,和原来的方向相同(即拐弯前后的两条路互相平行),若测得第一次拐弯的∠B是142°,则第二次拐弯的∠C应是多少度才合理?为什么?DCEFAAGG12小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?①两直线被第三条直线所截,同位角相等。②两直线平行,同旁内角相等。③“内错角相等,两直线平行”是平行线的性质。④“两直线平行,同旁内角互补”是平行线的性质。×√××判断下列语句是否正确①DE、BC平行吗?为什么?②∠C等于多少度?为什么?ACBED解: ∠ADE=60°,∠B=60°(同位角相等,两直线平行)(两直线平行,同位角相等)(等量代换)∴∠ADE=∠B∴DEBC∥∴∠C=∠AED又 ∠AED=80°(已知)∴∠C=80°2、如图,已知D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=80°ABCD解: AD∥BC(已知)∴A+B=180°即∠B=180°-A=180°-115°=65° AD∥BC(已知)∴D+C=180°即C=180°-D=180°-100°=80°答:梯形的另外两个角分别为65°、80°例1、如图有一块梯形的玻璃,已知量得∠A=115°,∠D=100°,请你想一想,梯形的另外两个角各是多少度。(两直线平行,同旁内角互补)(两直线平行,同旁内角互补)1、如图: ∠1=∠2()∴AD∥()∴∠BCD+=180°()ABCD12已知BC∠D内错角相等,两直线平行两直线平...