一元二次方程根的判别式-(4)VIP免费

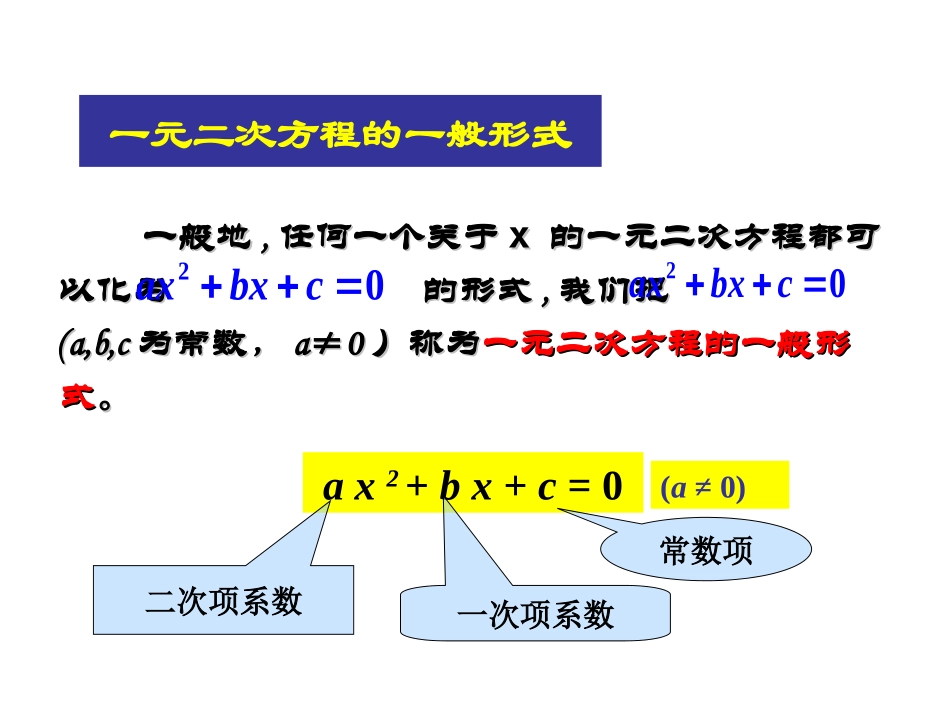
ax2+bx+c=0(a≠0)二次项系数一次项系数常数项一元二次方程的一般形式一般地一般地,,任何一个关于任何一个关于xx的一元二次方程都可的一元二次方程都可以化为的形式以化为的形式,,我们把我们把(a,b,c(a,b,c为常数，为常数，a≠0a≠0）称为）称为一元二次方程的一般形一元二次方程的一般形式式。。20axbxc20axbxc1、判断下面哪些方程是一元二次方程222221x2y24(1)x-3x+4=x-7()(2)2X=-4()(3)3X+5X-1=0()(4)3x-20()(5)13()(6)0()xy√√××××练习二2、把方程（1-x)(2-x)=3-x2化为一般形式是：___________,其二次项系数是____,一次项系数是____,常数项是____.3、方程（m-2)x|m|+3mx-4=0是关于x的一元二次方程，则（）A.m=±2B.m=2C.m=-2D.m≠±22x2-3x-1=02-3-1C4、关于x的方程(a2-4)x2+(a+2)x-1=0(1)当a取什么值时,它是一元一次方程?(2)当a取什么值时,它是一元二次方程?a2-4=0a+2≠0解:(1)∴a=2∴当a=2时，原方程是一元一次方程(2)a2-4≠0∴a≠±2∴当a≠±2时，原方程是一元二次方程你学过一元二次方程的哪些解法?因式分解法开平方法配方法公式法例:解下列方程•１、用直接开平方法：(x+2)2=９•2、用配方法解方程：4x2-8x-5=03、用公式法解方程:3x2=4x+74、用分解因式法解方程：（y+2)2=3(y+2）一元二次方程的基本解法配方法直接开平方法因式分解法公式法提取公因式法平方差公式完全平方公式……你能说出每一种解法的特点吗?方程的左边是完全平方式,右边是非负数;即形如x2=a(a≥0)ax,ax21用公式法解一元二次方程的前提是:1.必需是一般形式的一元二次方程:ax2+bx+c=0(a≠0).2.b2-4ac≥0..04acb.2a4acbbx221.(2005福州中考)解方程:(x+1)(x+2)=62.(2005北京中考)已知:(a2+b2)(a2+b2-3)=10求a2+b2的值。3.解下列方程（1）x2=0(2)x(x-6)=-2(x-6)4.(2004武汉中考)试证明关于x的方程(a2-a+2)x2+ax+2=0无论a取何值,该方程都是一元二次方程.中考直击思考2221221214044222402340acbbacbbac.aa()bac,;b.a()bac,.xxxx2（）当b时，一元二次方程有两个不相等的实数根；，当时一元二次方程有两个相等的实数根当时一元二次方程没有实数根一元二次方程的根与系数：根的判别式：b2-4ac练习：•1、方程2x2+3x－k=0根的判别式是；当k时，方程有实根。•2、方程x2+2x+m=0有两个相等实数根，则m=。•3、关于x的方程x2-(2k-1)x+(k-3)=0.试说明无论k为任何实数,总有两个不相等的实数根.•4、关于x的一元二次方程mx2+(2m－1)x－2=0的根的判别式的值等于4，则m=。一元二次方程的根与系数的关系：若ax2+bx+c=0的两根为x1、x2，则x1+x2=_______；x1x2=___；以x1、x2为根（二次项系数为1）的一元二次方程为_________________.x2-(x1+x2)x+x1x2=0abac一元二次方程的根与系数：韦达定理：已知两数的和是4,积是1，则此两数为.拓展练习：•１、已知方程x2－mx+2=0的两根互为相反数，则m=。•2、已知方程x2+4x－2m=0的一个根α比另一个根β小4，则α=；β=；m=.•3、已知方程5x2+mx－10=0的一根是－5，求方程的另一根及m的值。•4、关于x的方程2x2－3x+m=0，当时，方程有两个正数根；当m时，方程有一个正根，一个负根；当m时，方程有一个根为0。.)1(,2的完全平方式是关于二次三项式为何值时xkxkkx的完全平方式。是关于）（时，当则有两个相等的实数根，）（解：若方程）（）（xxkxkkkkkkxkxxxkkx1122222212111012401,112xx.618.0251ABAC黄金比.1,,1xCBxACAB则设ABC.012xx即得解这个方程,.251x).,(251,25121舍去不合题意xx如图,点C把线段AB分成两条线段AC和BC,如果那么称线段AB被点C黄金分割(goldensection),点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.,ACBCABAC列一元二次方程解应用题的步骤与列一元一次方程解应用题的步骤类似，即审、设、列、解、验、答．几何与方程•1.将一块正方形的铁皮四角剪去一个边长为4cm的小正方形,做成一个无盖的盒子.已知盒子的容积是400cm3,求原铁皮的边长.快乐学习55得根据...