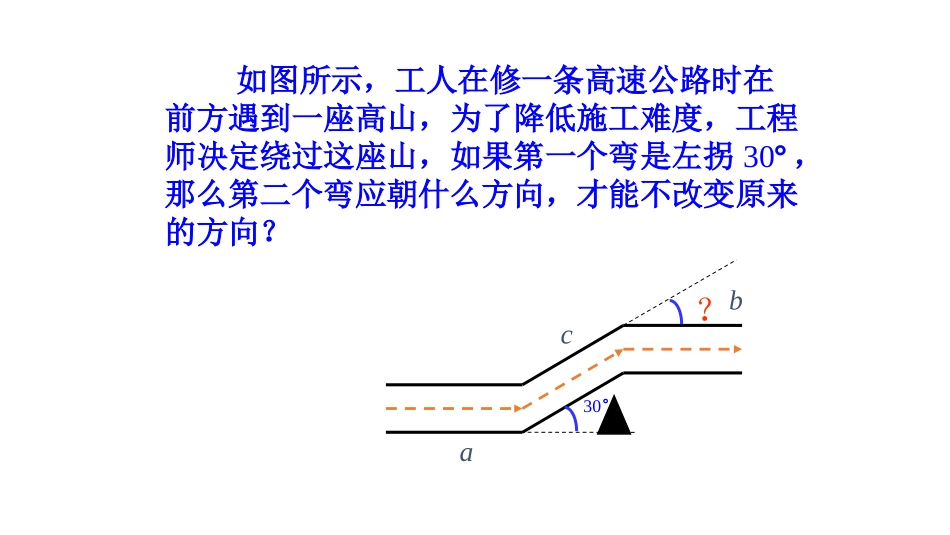
第七章平行线的证明如图所示,工人在修一条高速公路时在前方遇到一座高山,为了降低施工难度,工程师决定绕过这座山,如果第一个弯是左拐30°,那么第二个弯应朝什么方向,才能不改变原来的方向?ac?b30°知识回顾1、平行线的判定:(1)公理:同位角相等,两直线平行;(2)定理:内错角相等,两直线平行;(3)定理:同旁内角互补,两直线平行.2、定理:(1)对顶角相等;(2)在平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行.已知:如图所示,直线AB∥CD,∠1和∠2是直线AB,CD被直线EF截出的同位角。求证:∠1=∠2.ABCDEFMN12(1)∠1和∠2在数量关系上有哪两种情况?(2)过直线外一点有几条直线与这条直线平行?(1)∠1和∠2在数量关系上有哪两种情况?(2)过直线外一点有几条直线与这条直线平行?ABCDEFMNGH12证明:假设∠1≠2∠,过点M作直线GH,使∠EMH=∠2,如图所示.“”根据同位角相等,两直线平行,可知GH∥CD.又因为ABCD∥,这样经过点M存在两条直线AB和GH都与直线CD平行.“这与基本事实过直线外一点有且只有一条直”线与这条直线平行相矛盾.这说明∠1≠2∠的假设不成立,所以∠1=2∠.两直线平行,同位角相等.根据同位角相等可以判定两直线平行,反过来,如果两直线平行,同位角之间有什么关系呢?内错角、同旁内角之间又有什么关系呢?已知,如图,直线ab,1∥∠和∠2是直线a、b被直线c截出的内错角.求证:∠1=2.∠证明:∵ab∥(已知),∴∠3=2∠(两直线平行,同位角相等).∵∠1=3∠(对顶角相等),∴∠1=2∠(等量代换).两直线平行,内错角相等.已知,如图,直线ab∥,∠1和∠2是直线a、b被直线c截出的同旁内角.求证:∠1+2=180∠°.证明:∵ab∥(已知),∴∠3=2∠(两直线平行,同位角相等)。∵∠1+3=180°∠(1平角=180°),∴∠1+2=180∠°(等量代换)。两直线平行,同旁内角互补.3平行线的判定平行线的性质条件结论条件结论同位角相等两直线平行两直线平行同位角相等内错角相等两直线平行两直线平行内错角相等同旁内角互补两直线平行两直线平行同旁内角互补两条直线被第三条直线所截.例1例1已知:如图,ba∥,ca∥,∠1,∠2,∠3是直线a,b,c被直线d截出的同位角.求证:bc.∥abc123d证明:∵证明:∵ba∥ba∥(已知)(已知)∴∠∴∠2=1∠2=1∠(两直线平行,同位角相等)(两直线平行,同位角相等)∵∵ca∥ca∥(已知)(已知)∴∠∴∠3=1∠3=1∠(两直线平行,同位角相等)(两直线平行,同位角相等)∴∠∴∠2=3∠2=3∠(等量代换)(等量代换)∴∴bc∥bc∥(同位角相等,两直线平行)(同位角相等,两直线平行)定理:平行于同一条直线的两条直线平行定理:平行于同一条直线的两条直线平行..定理:平行于同一条直线的两条直线平行定理:平行于同一条直线的两条直线平行..(1)证明的一般步骤:①理解题意;②根据题意正确画出图形;③结合图形,写出“已知”和“求证”;④分析题意,探索证明的思路;⑤依据寻求的思路,运用数学符号和数学语言条理清晰地写出证明过程;⑥检查表达过程是否正确、完善.完成一个定理的证明,需要哪些环节?完成一个定理的证明,需要哪些环节?例题讲解如图所示,AB∥CD,∠CDE=140°,则∠A的度数为()A.140°B.60°C.50°D.40°D1.平行线的性质定理有:,,。检测反馈两直线平行,同位角相等2.如图所示,∠4=∠C,∠1=∠2,求证BD平分∠ABC.证明:∵∠4=∠C,∴AD∥BC,∴∠2=∠3.又∵∠1=∠2,∴∠1=∠3,即BD平分∠ABC.两直线平行,内错角相等两直线平行,同旁内角互补1.(郴州·中考)下列图形中,由ABCD∥,能得到∠1=2∠的是()B2.(常德·中考)如图,已知直线ABCD∥,直线EF与直线AB、CD分别交于点E、F,且有∠1=70°,则∠2=____.【解析】由AB∥CD可得出∠2=∠AEF,因∠1+∠AEF=180°,∠1=70°,可得出∠AEF=110°,所以∠2=110°.答案:110°3.(中山·中考)如图,已知∠1=70°,如果CD//BE,那么∠B的度数为____.【解析】由平行线的性质和对顶角的性质易得∠B=110°.答案:110°课堂小结两直线平行两直线平行同位角相等同位角相等内错角相等内错角相等同旁内角互补同旁内角互补性质定理平行于同一直线的两条直线平行平行于同一直线的两条直线平行