探究与发现利用单位圆中的三角函数线研究正弦函数、余弦函数的性质VIP免费

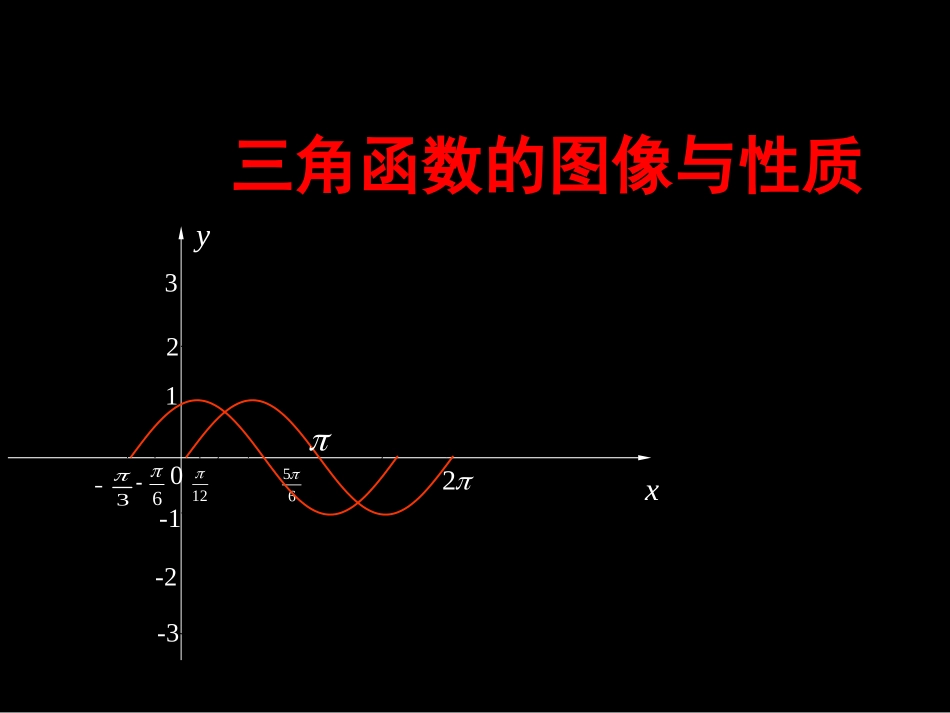
三角函数的图像与性质xy2656123321-3-2-10已知函数2131()cossincos,224fxxxxxR作业点评作业点评例题讲解练习反馈课堂心得作业布置0xy00026x322212651223111212121sin(2)26x原函数可化为f(x)(6)画出函数在区间上的图像[,]220.5log()yfx(3)求函数的单调递增区间.例1.(06湖北高考)设向量(cos,cos),,bxxxR函数()()fxaab（1）求函数的最大值与最小正周期；(sin,cos),axx()fx（2）求使不等式成立的的x取值集合.3()2fx例题讲解作业点评例题讲解练习反馈课堂心得作业布置例2.关于函数有下列命题：()4sin(2)()3fxxxR12xx①由，可得必是的整数倍；12()()0fxfx②的表达式可改写为③的图像关于（）对称；④的图像关于直线对称.其中正确的命题的序号是()yfx4cos(2)6yx()yfx,06()yfx6x作业点评例题讲解练习反馈课堂心得作业布置温馨提示温馨提示::1.1.将将4sin(2)sin3yxyx2.2.函数函数f(x)f(x)的对称中心就是函数的对称中心就是函数图像与坐标轴的交点图像与坐标轴的交点;;3.3.在对称轴处函数值取到最值在对称轴处函数值取到最值例3.（03江苏高考）已知函数是R上的偶函数，其图像关于点M（）对称，且在区间上是单调函数，求的值.()sin()(0,0)fxx3,04[0,]2和作业点评例题讲解练习反馈课堂心得作业布置心中有图,0,cos0.x对任意都成立且所以得0,.2由题设解得(),()()fxfxfx由是偶函数得sin()sin().xx即sincossincos.xx所以练习反馈sin(0)yx（A）（B）（C）（D）1.（06安徽）将函数的图像按向量平移，平移后的图像如图所示，则平移后的图像所对应的函数解析式是（）(,0)6asin()6yxsin()6yxsin(2)3yxsin(2)3yx作业点评例题讲解练习反馈课堂心得作业布置C2.如果函数的图像关于直线对称，那么的值为（）（A）（B）（C）1（D）-1sin2cos2yxax8xa22作业点评例题讲解练习反馈课堂心得作业布置D课堂心得作业点评例题讲解练习反馈课堂心得作业布置1.化归的思想方法sin()sinyAxyx高次、多项2.数形结合的思想方法数缺形时少直观,形少数时难入微.数形结合百般好,割裂分家万事休.作业布置《导与练》必做：第21页例4，第22页1、3、5、6、7、11、12选做：第21页例3作业点评例题讲解练习反馈课堂心得作业布置