1352线段的垂直平分线VIP免费

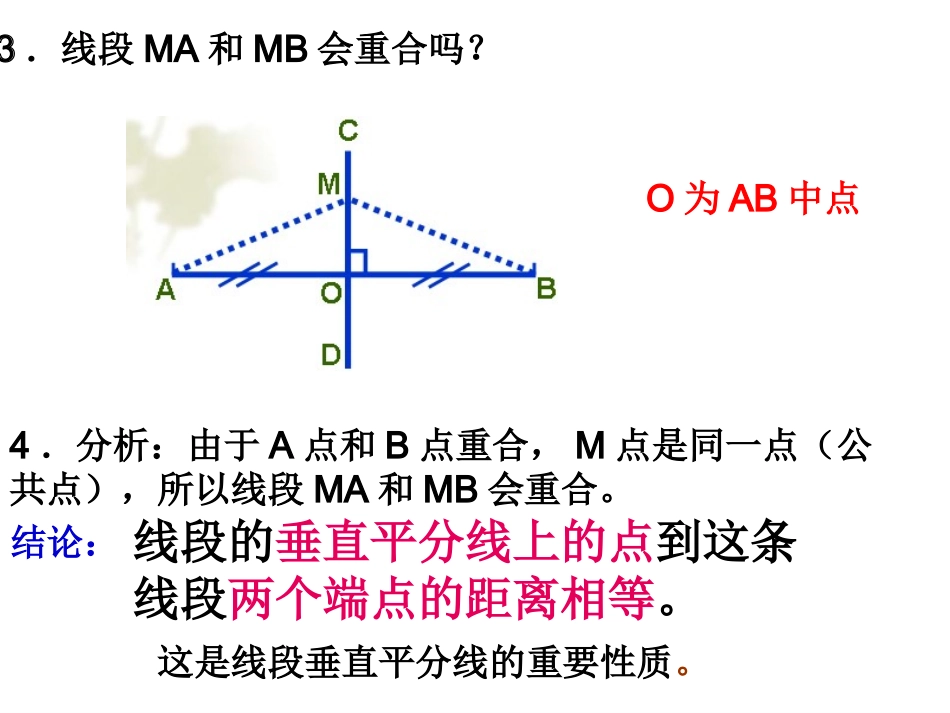
13.5.2线段的垂直平分线回忆与思考1、什么叫线段垂直平分线？经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也叫中垂线。2、线段是不是轴对称图形？O为AB中点3．线段MA和MB会重合吗？4．分析：由于A点和B点重合，M点是同一点（公共点），所以线段MA和MB会重合。线段的垂直平分线上的点到这条线段两个端点的距离相等。结论：这是线段垂直平分线的重要性质。直线MNAB，垂足是C，且AC=CB.点P在MN上.已知：PA=PB求证：ABCNMP证明: MNAB（已知）∴PCA=PCB(垂直的定义)在PCA和PCB中,AC=CB(已知),PCA=PCB(已证)PC=PC(公共边)∴PCA≌PCB(SAS)∴PA=PB(全等三角形的对应边相等)ABCMNPABCMNP当点P与点C重合时,上述证明有什么缺陷?PCA与PCB将不存在.PA与PB还相等吗?相等!此时,PA=CA,PB=CB已知AC=CB∴PA=PBABCMN线段垂直平分线上的点到这条线段两个端点的距离相等.性质定理例2.△ABC中，BC＝10，边BC的垂直平分线分别交AB、BC于点E、D；BE＝6，求△BCE的周长。解： ED是BC的垂直平分线（已知）∴EC＝EB=6（线段的垂直平分线上的点到这条线段两个端点的距离相等）∴△BCE的周长=BC＋CE＋EB＝10＋6＋6=22例2.ABC△中，BC＝10，边BC的垂直平分线分别交AB、BC于点E、D；BE＝6，求△BCE的周长。那么到线段两端点距离相等的点是否一定在线段的中垂线上？ABPC已知:线段AB,且PA=PB求证:点P在线段AB的垂直平分线MN上.过点P作PCAB垂足为C. PA=PB(已知)∴PAB是等腰三角形(等腰三角形的定义)∴AC=BC(等腰三角形底边上的高是底边上的中线)∴PC是线段AB的垂直平分线.即点P在线段AB的垂直平分线MN上.证明:到线段两个端点距离相等的点,在这条线段的垂直平分线上.判定定理该定理只能判定一个点在线段的中垂线上，那么如何判定一条直线是线段的中垂线呢？要证明几个点在线段的中垂线上呢？因为两点确定一条直线，我们只需证明这条直线上有两个点到线段两端点的距离相等，即有两个点在线段的中垂线上。小结:1.性质定理：线段的垂直平分线上的点,到这条线段两个端点的距离相等.2.判定定理：到线段两个端点距离相等的点,在这条线段的垂直平分线上.互逆定理能否根据线段的垂直平分线的性质定理和判定定理，来证明三角形三边的垂直平分线交于一点？ACBMPNM/N/思路：证其中两条中垂线的交点，也在第三条中垂线上。ACBMPN证明： PM、PN分别是AB、BC的垂直平分线()∴PA=PB,PB=PC()∴PA=PC()∴点P在AC的垂直平分线()作图题:如图,在直线l上求一点P,使PA=PBlBAP点P为所求作的点问题:如图,A、B、C三个村庄合建一所学校,要求校址P点距离三个村庄都相等.请你帮助确定校址.ABCP点P为校址填空：1.已知:如图,AD是ABC的高,E为AD上一点,且BE=CE,则ABC为三角形.2.已知:等腰ABC,AB=AC,AD为BC边上的高,E为AD上一点,则BEEC.(填>、<或=号)ABCEDABCED1题图2题图等腰=3.已知:如图,AB=AC,A=30o,AB的垂直平分线MN交AC于D,则BDC=,DBC=.ABCDMN30o1275o30o60o45o填空：4.已知:如图,在ABC中,DE是AC的垂直平分线,AE=3cm,ABD的周长为13cm,则ABC的周长为cmABDCE3cm3cm1913cm证明题:1.已知:ABC中,C=90,A=30o,BD平分ABC交AC于D.求证:D点在AB的垂直平分线上.ABCD证明:30o C=90o,A=30o(已知)∴ABC=60o(三角形内角和定理)∴A=ABD(等量代换)∴D点在AB的垂直平分线上 BD平分ABC(已知)∴ABD=30o(角平分线的定义)30o∴AD=BD(等角对等边)证明题:2.已知:如图,线段CD垂直平分AB,AB平分CAD.求证:ADBC.∥ABCDO123证明: 线段CD垂直平分AB∴CA=CB∴1=3又 AB平分CAD∴1=2∴2=3∴ADBC∥4.已知:如图,AD平分BAC,EF垂直平分AD交BC的延长线于F,连结AF.求证:CAF=B.ABCDEFABCDEF123∴1+CAF=3又 3=B+2∴1+CAF=B+2 AD平分BAC∴2=1∴CAF=B.证明:EF 垂直平分AD∴AF=DF∴DAF=3变式1如图,在△ABC中∠c=90,DE垂直平分AB,分别交AB,BC于点D,E,若∠EAC:EAB=7:4,∠求∠B的度数解： DE垂直平分ABEA=EB∴∴∠EAB=B∠EAC ∠：∠EAB=4：7EAC∴∠：∠EAB：∠B=4：7：...