同分母分式的加减法VIP免费

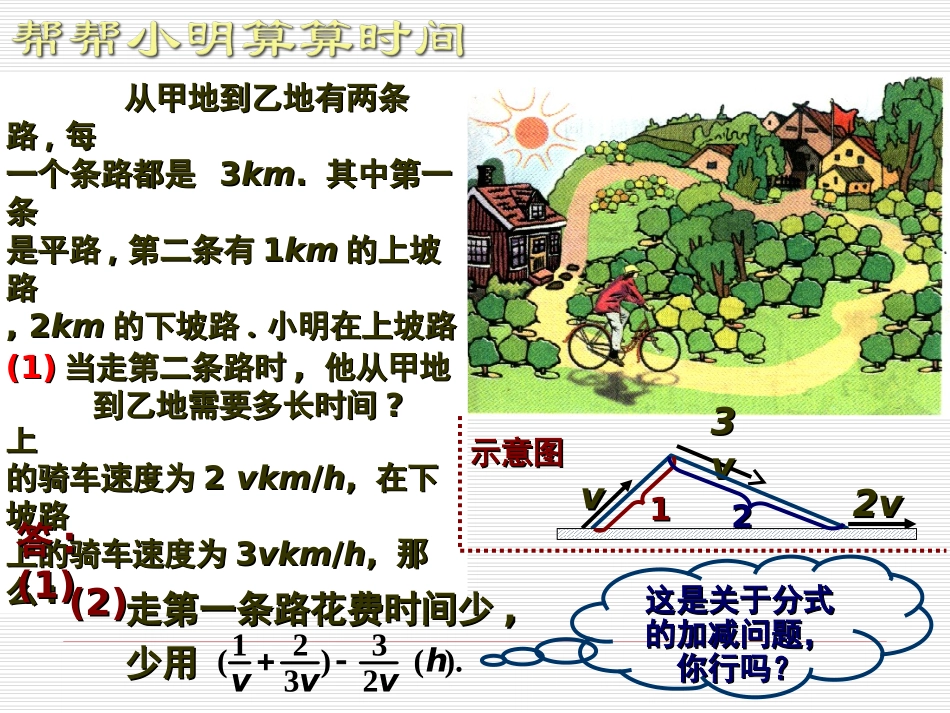
课首课首课首课首北师大北师大••八年级八年级《《数学数学((下下))》》5.3分式的加减法(1)5.3分式的加减法(1)经历探索分式的加减运算法则的过程经历探索分式的加减运算法则的过程,,理解其算理；理解其算理；通分后对分式的化简通分后对分式的化简..难点难点::重点重点::分式的加减法则、分式的加减法则、通分、化简通分、化简..能解决一些简单的实际问题，能解决一些简单的实际问题，进一步体会分式的模型作用进一步体会分式的模型作用..会进行简单分式的加减运算会进行简单分式的加减运算,,具有一定的代数化归能力具有一定的代数化归能力..)(321hvv).(23)321(hvvv这是关于分式这是关于分式的加减问题，的加减问题，你行吗？你行吗？(2)(2)他走哪条路花费时间少他走哪条路花费时间少??少用多长时间少用多长时间??从甲地到乙地有两条从甲地到乙地有两条路路,,每每一个条路都是一个条路都是33kmkm..其中第一其中第一条条是平路是平路,,第二条有第二条有11kmkm的上坡的上坡路路,2,2kmkm的下坡路的下坡路..小明在上坡路小明在上坡路上上的骑车速度为的骑车速度为vkmvkm//hh,,在平路在平路上上的骑车速度为的骑车速度为22vkmvkm//hh,,在下在下坡路坡路上的骑车速度为上的骑车速度为33vkmvkm//hh,,那那么么::(1)(1)当走第二条路时当走第二条路时,,他从甲地他从甲地到乙地需要多长时间到乙地需要多长时间??答答::(1)(1)(2)(2)走第一条路花费时间少走第一条路花费时间少,,少用少用vv33vv2v2v示意图示意图1122?5251:如?21aa22、、你认你认为为33、、猜一猜猜一猜,,同分母的分式应该如何加同分母的分式应该如何加减减??11、、同分母分数加减法的法则是什么？同分母分数加减法的法则是什么？想一想想一想分母不变分母不变,,分子相加减分子相加减..【【同分母的分数加减法的法则同分母的分数加减法的法则】】同分母的分数相加减，同分母的分数相加减，同分母分式加减法法则与同分母分数加减法的法则类似同分母分式加减法法则与同分母分数加减法的法则类似【【同分母的分式加减法的法则同分母的分式加减法的法则】】同分母的分式相加减，同分母的分式相加减，分母不变分母不变,,分子相加减分子相加减..尝试完成下列各题：做一做做一做做一做做一做P72P72?242)1(2xxx?131112)2(xxxxxx.2222242xxxxxx.113121312xxxxxxxxxx?20153:如?413aa比如22、、你认为异分母的分式应该如何加你认为异分母的分式应该如何加减减??11、、异分母的分数如何加减？异分母的分数如何加减？想一想想一想【【异分母的分数加减的法则异分母的分数加减的法则】】【【异分母的分数加减的法则异分母的分数加减的法则】】先先通分，把异分母分数通分，把异分母分数化为同分母的分数，化为同分母的分数，然后再按同分母分数的然后再按同分母分数的加减法法则进行计算。加减法法则进行计算。异分母分式加减法法则与异分母分数加减法的法则类似异分母分式加减法法则与异分母分数加减法的法则类似异分母分式加减法法则与异分母分数加减法的法则类似异分母分式加减法法则与异分母分数加减法的法则类似【【异分母的分式加减的法则异分母的分式加减的法则】】【【异分母的分式加减的法则异分母的分式加减的法则】】先先通分，把异分母分式通分，把异分母分式化为同分母的分式，化为同分母的分式，然后再按同分母分式的然后再按同分母分式的加减法法则进行计算。加减法法则进行计算。小明认为小明认为,,只要所异分母的分式化成同分母的分式只要所异分母的分式化成同分母的分式,,异分母的分式的问异分母的分式的问题就变成了同分母分式的加减问题题就变成了同分母分式的加减问题..小亮同意小明的这种看法小亮同意小明的这种看法,,但他俩的具体但他俩的具体做法不同：做法不同：aa413aa41443.41341412aaaaa413aaaaa4443224412aaaa2413aa;413a你对这两种做法有何评判你对这两种做法有何评判??根据分式的基本性质根据分式的基本性质,,异分母的分式可化为异分母的分...