必修4角的和差倍章章末复习课件VIP免费

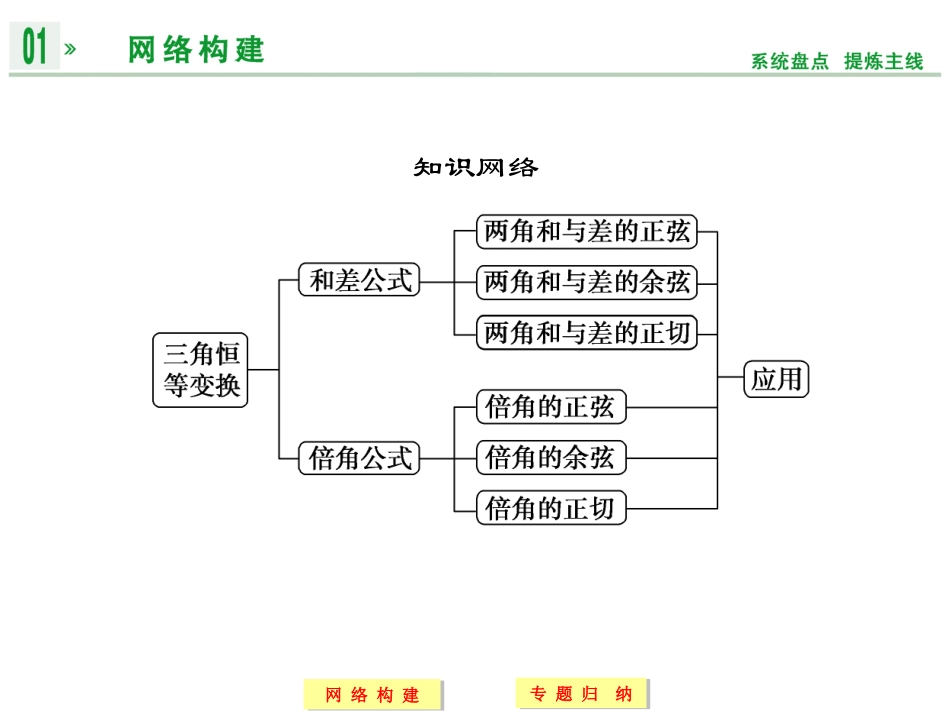
网络构建网络构建专题归纳专题归纳章末复习课网络构建网络构建专题归纳专题归纳知识网络网络构建网络构建专题归纳专题归纳要点归纳1．本章的公式多不易记住，解决这个问题的最好办法就是掌握每个公式的推导过程：首先用向量方法推导出C(α－β)，再用－β代替C(α－β)中的β得到C(α＋β)；接着用诱导公式sin(α±β)＝cosπ2－α±β＝cosπ2－α∓β得到S(α＋β)与S(α－β)；将S(α＋β)除以C(α＋β)得到T(α＋β)，将S(α－β)除以C(α－β)得到T(α－β)；将S(α＋β)、C(α＋β)、T(α＋β)中的β换为α，得到S2α、C2α、T2α.网络构建网络构建专题归纳专题归纳2．熟练掌握常用的角的变换，是提高解题速度、提高分析问题和解决问题的能力的有效途径．常用的角的变换有：α＝2·α2、4α＝2·2α、π4－α2＝π2－α2、2α＝(α＋β)＋(α－β)＝(α＋β)－(β－α)、2β＝(α＋β)－(α－β)＝(α＋β)＋(β－α)、α＝(α＋β)－β＝β－(β－α)、β＝α＋β2－α－β2、α＋β2＝α－β2－α2－β、α－β2＝α＋β2－α2＋β.这些变换技巧需要同学们在平时解题的过程中多多摸索，而探索的方法就是认真观察已知条件中的角与待求式中的角之间的关系．网络构建网络构建专题归纳专题归纳3．时刻注意考虑角的范围是避免解题出错的唯一方法，首先是本章的某些公式中的角就有范围限制，如tan2α＝2tanα1－tan2α中的α的限制条件是α≠kπ＋π2且α≠kπ2＋π4(k∈Z)；其次是题中的角的范围也是有限制的.网络构建网络构建专题归纳专题归纳专题一三角函数式的化简三角函数式的化简，主要有以下几类：①对和式，基本思路是降幂、消项和逆用公式；②对分式，基本思路是分子与分母的约分和逆用公式，最终变成整式或数值；③对二次根式，则需要运用倍角公式的变形形式．在具体过程中体现的则是化归的思想，是一个“化异为同”的过程，涉及切弦互化，即“函数名”的“化同”；角的变换，即“单角化倍角”“单角化复角”“复角化复角”等具体手段．网络构建网络构建专题归纳专题归纳【例1】化简：sin2αsin2β＋cos2αcos2β－12cos2αcos2β.解法一原式＝sin2αsin2β＋cos2αcos2β－12(2cos2α－1)·(2cos2β－1)＝sin2αsin2β＋cos2αcos2β－12(4cos2αcos2β－2cos2α－2cos2β＋1)＝sin2αsin2β－cos2αcos2β＋cos2α＋cos2β－12＝sin2αsin2β＋cos2α(1－cos2β)＋cos2β－12＝sin2αsin2β＋cos2αsin2β＋cos2β－12网络构建网络构建专题归纳专题归纳＝sin2β(sin2α＋cos2α)＋cos2β－12＝sin2β＋cos2β－12＝1－12＝12.法二原式＝sin2αsin2β＋(1－sin2α)cos2β－12cos2αcos2β＝cos2β－sin2α(cos2β－sin2β)－12cos2αcos2β＝cos2β－sin2αcos2β－12cos2αcos2β＝cos2β－cos2βsin2α＋12cos2α网络构建网络构建专题归纳专题归纳＝1＋cos2β2－cos2βsin2α＋121－2sin2α＝1＋cos2β2－12cos2β＝12.法三原式＝1－cos2α2·1－cos2β2＋1＋cos2α2·1＋cos2β2－12cos2αcos2β＝14(1＋cos2αcos2β－cos2α－cos2β)＋14(1＋cos2αcos2β＋cos2α＋cos2β)－12cos2αcos2β＝14＋14＝12.网络构建网络构建专题归纳专题归纳法四原式＝(sinαsinβ－cosαcosβ)2＋2sinαsinβ·cosαcosβ－12cos2αcos2β＝cos2(α＋β)＋12sin2αsin2β－12cos2αcos2β＝cos2(α＋β)－12cos(2α＋2β)＝cos2(α＋β)－12[2cos2(α＋β)－1]＝12.网络构建网络构建专题归纳专题归纳专题二三角函数求值三角函数求值主要有三种类型，即(1)“给角求值”，一般给出的角都是非特殊角，观察发现题中的角与特殊角都有着一定的关系，如和或差为特殊角，必要时运用诱导公式．(2)“给值求值”，即给出某些角的三角函数式的值，求另外一些三角函数的值，这类求值问题关键在于结合条件和结论中的角，合理拆、配角．要注意角的范围．(3)“给值求角”，本质上还是“给值求值”，只不过往往求出的是特殊角的值，在求出角之前还需结合函数的单调性确定角...