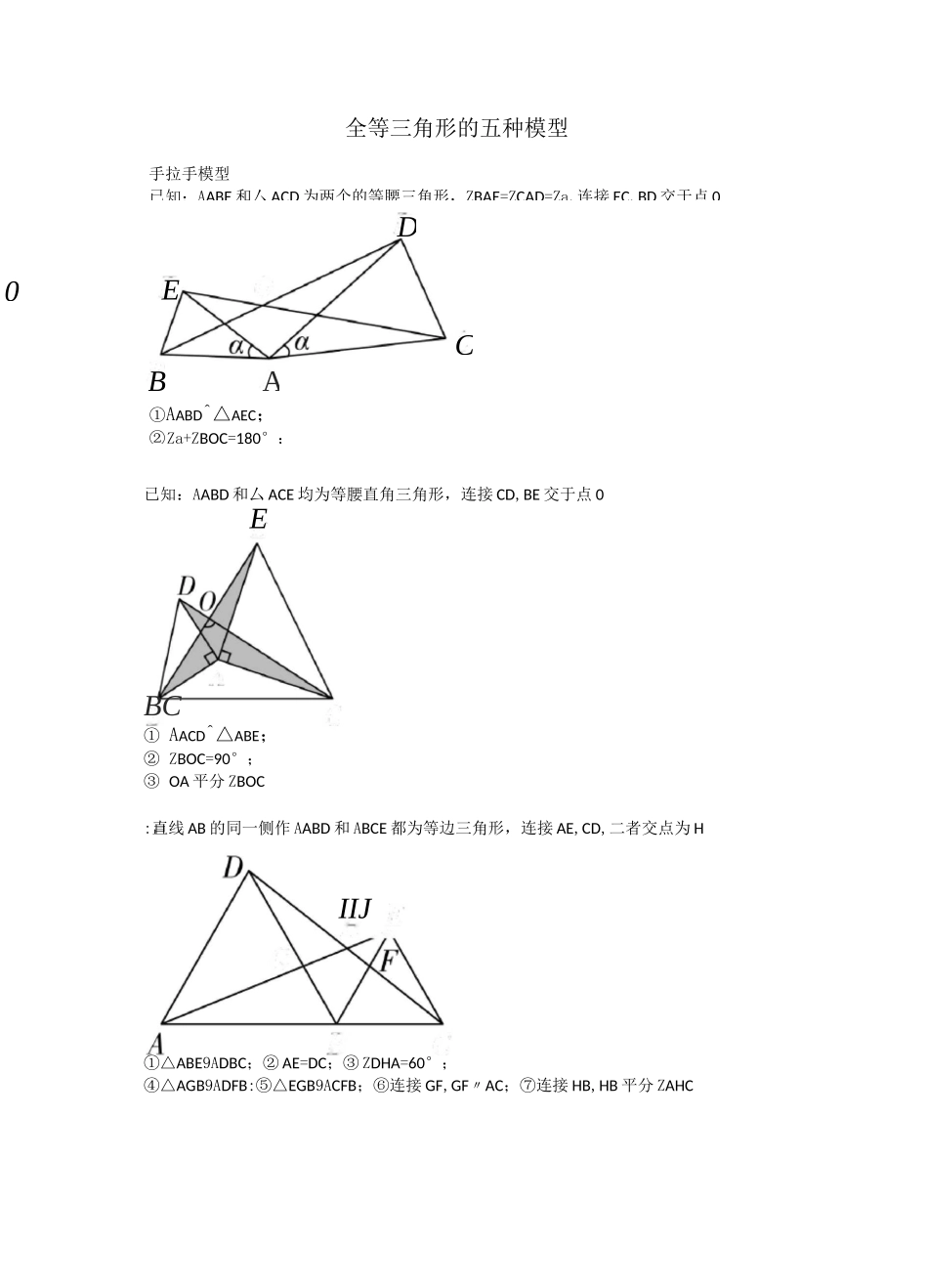
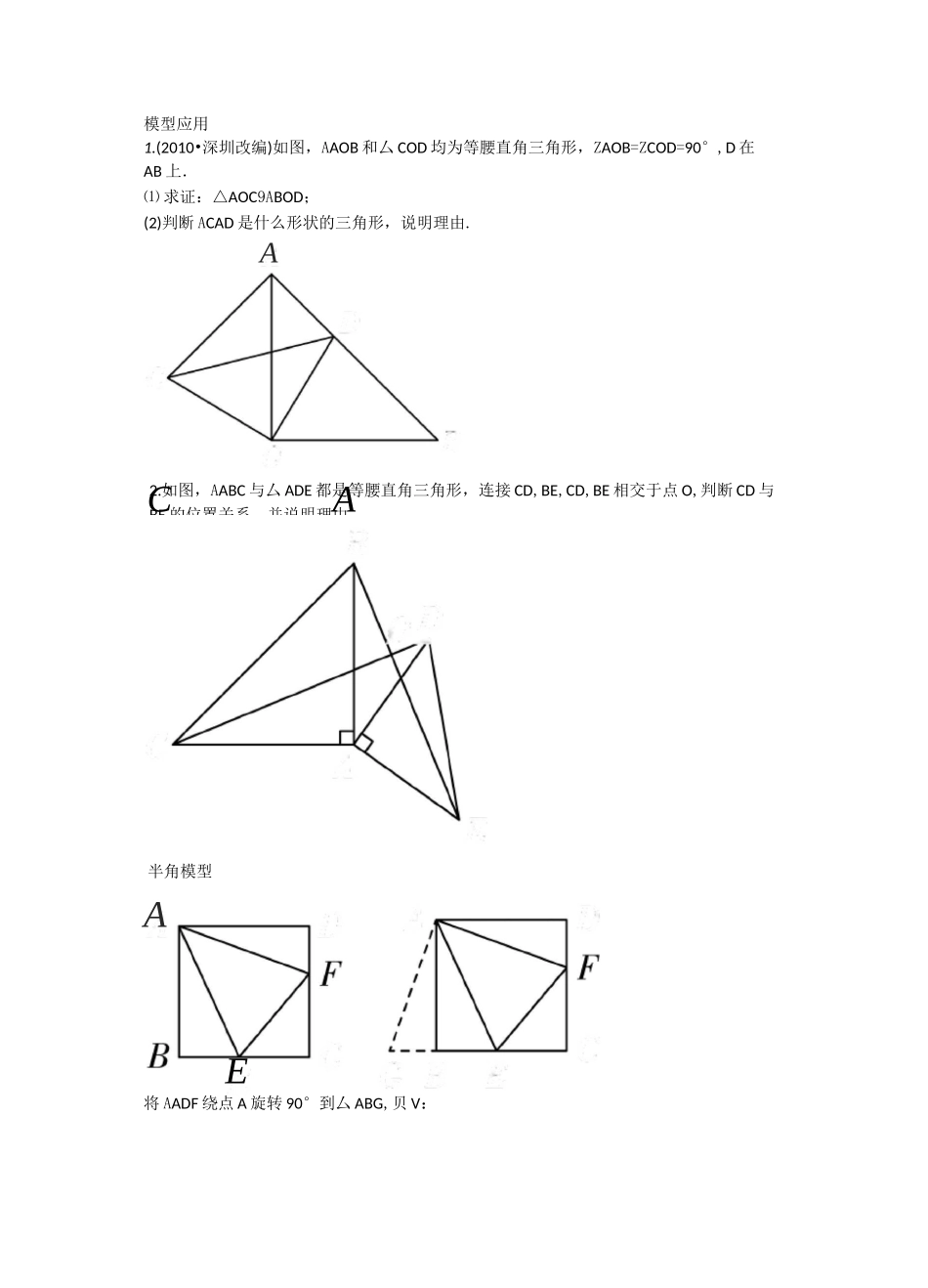
已全等三角形的五种模型已知:AABD和厶ACE均为等腰直角三角形,连接CD,BE交于点0EBC①AACD^△ABE;②ZBOC=90°;③OA平分ZBOC:直线AB的同一侧作AABD和ABCE都为等边三角形,连接AE,CD,二者交点为HIIJ①△ABE9ADBC;②AE=DC;③ZDHA=60°;④△AGB9ADFB:⑤△EGB9ACFB;⑥连接GF,GF〃AC;⑦连接HB,HB平分ZAHC手拉手模型已知:AABE和厶ACD为两个的等腰三角形,ZBAE=ZCAD=Za,连接EC,BD交于点0D0ECBA①AABD^△AEC;②Za+ZBOC=180°;BCAEOP2.如图,AABC与厶ADE都是等腰直角三角形,连接CD,BE,CD,BE相交于点O,判断CD与BE的位置关系,并说明理由.半角模型已知:正方形ABCD中,E,F分别是BC,CD边上的点,且ZEAF=45模型应用1.(2010•深圳改编)如图,AAOB和厶COD均为等腰直角三角形,ZAOB=ZCOD=90°,D在AB上.⑴求证:△AOC9ABOD;(2)判断ACAD是什么形状的三角形,说明理由.AAE将AADF绕点A旋转90°到厶ABG,贝V:①EF=DF+BE;②ACEF的周长为正方形ABCD周长的一半已知:正方形ABCD中,E,F分别是BC,CD边上的点,且ZEAF=45DEfcF将AAEB绕点A为旋转90°到厶ADE',贝V:EF=DF—BE已知:在正方形ABCD中,AB=1,E,F分别是边BC,CD上的点,连接EF,AE,AF,过A作AH丄EF于点H,BE=EH①△ABE^AAHE;②△AHF^AADF;③ZEAF=45°;④EF=BE+DF模型应用3.(2015•深圳改编)如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG9AFDG;②GB=2AG:③ZGDE=45°:④DG=DE.在以上4个结论中,正确的共有()A.1个B.2个C.3个D.4个EC4.如图,在正方形ABCD中,AB=1,E,F分别是边BC,CD上的点,连接EF,AE,AF,过A作AH丄EF于点H.若EF=BE+DF,那么下列结论:①AE平分ZBEF;②FH=FD:③ZEAF=45°:④S^EAF=S^ABE+S^ADF:⑤ACEF的周长为2.其中正确结论的个数是()A.2B.3C.4D.5ADHCBE倍长中线模型已知:在AABC中,AD是BC边中线延长AD到E,使DE=AD,连接BE,则:①△ADC9AEDB;1②AD<2(AB+AC)已知:在AABC中,AD是BC边中线作CF丄AD于F,作BE丄AD的延长线于E,连接BE,则:①△BDE9ACDF;②BE〃FC模型应用5.(2014朋圳)如图,已知四边形ABCD为等腰梯形,.4I)//B(:\AB=CD,AD=\壮,"CD中点,连接,匹,fl.AE=2-\l3,ZD4£=3(巴AE丄彳尸交£?C于F,则BF=()A.1B.3—\卜C.\/5-1D.4-2A/26.已知:在厶ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF.D一直线三垂直模型已知:AE=DE,AE丄DE,ZB=ZC=90°①△ABE^AECD;②BC=AB+CD已知:在正方形ABCD中,ZABF=ZC=90°,AF丄BE,交于点H①△ABF^ABCE;②EC=AB-FC模型应用7.(2016•深圳改编)如图,CB=CA,ZACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG丄CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;®S^FAB:S四边形CBFG=1:2:③ZABC=ZABF.其中正确的结论的个数是()A.1B.2C.3D.08.如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,则下列结论:①ZAME=90°:②ZBAF=ZEDB;③MD=2AM=4EM.其中正确的结论有()AD(:B第塔题9.如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE丄AG于点E,BF〃DE,父AG于点F.给出以下结论:①△AED94BFA;②DE-BF=EF;③△BGFs^DAE;④DE-BG=FG.其中正确的有()A.1个B.2个C.3个D.4个10.(2018•深圳)如图,四边形ACDF是正方形,ZCEA和ZABF都是直角且点E,A,B三点共线,AB=4,则阴影部分的面积是.对角互补模型已知ZAOB=ZDCE=90°,OC平分ZAOB过点C作CM丄AO,CE±BO,则:①△CATDMZXCAE;②CD=CE;(§)01)+OD=A/2;ODCE—SAOCD+S^OCE=2OC212.(2017•深圳)如图,在Rt^ABC中,ZABC=90°,AB=3,BC=4,Rt^MPN,ZMPN