双曲线的几何性质VIP免费

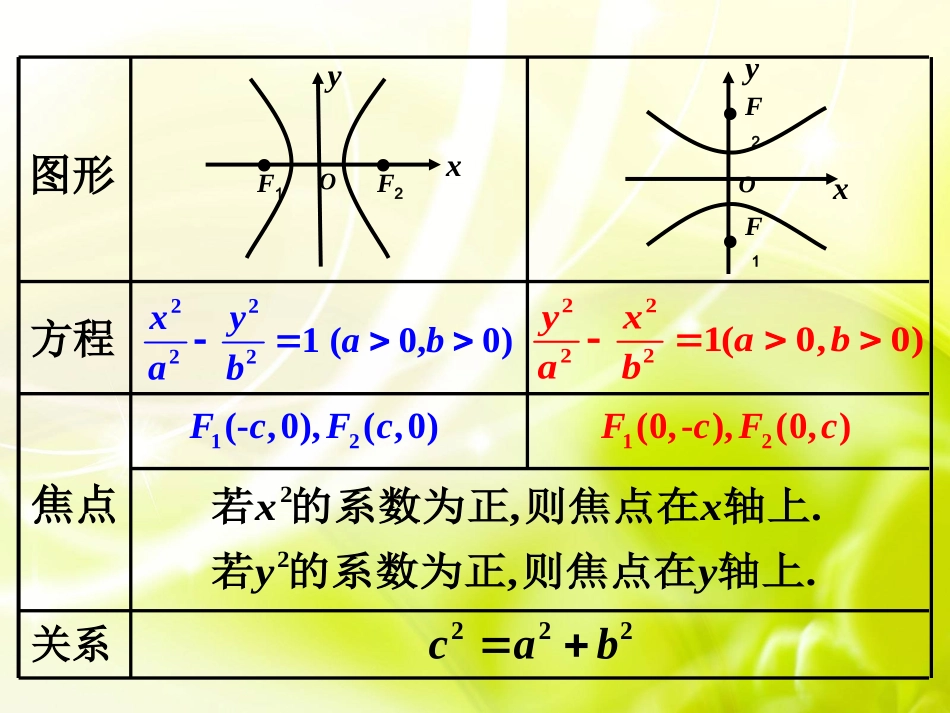
双曲线的几何性质19.2授课人：王群22221(0,0)xyabab22221(00)yxa,bab..yxOF2F1xyO.F2F1.焦点12(-,0),(,0)FcFc12(0,-),(0,)FcFc22,.,.xxyy若的系数为正则焦点在轴上若的系数为正则焦点在轴上关系222cab图形方程2、对称性一、研究双曲线的简单几何性质)0,0(12222babyax1、范围axax或关于x轴、y轴和原点都是对称。x轴、y轴是双曲线的对称轴，原点是对称中心，又叫做双曲线的中心。xyo-aa(-x,-y)(-x,y)(x,y)(x,-y)课堂新授课堂新授Ry3、顶点（1）双曲线与对称轴的交点，叫做双曲线的顶点xyo-b1B2Bb1A2A-aa12(,0)(,0)AaAa顶点是、只有两个！如图，线段叫做双曲线的实轴，它的长为2a,a叫做半实轴长；线段叫做双曲线的虚轴，它的长为2b,b叫做双曲线的半虚轴长2A1A2B1B（2）实轴与虚轴等长的双曲线叫等轴双曲线（3）)0(22mmyx4、离心率,cea双曲线的焦距与实轴长的比叫做双曲线的离心率 c>a>0∴e>1e是表示双曲线开口大小的一个量,e越大开口越大!（1）定义：（2）e的范围：（3）e的意义：221169xy双曲线(1)范围：44,xxyR或(2)顶点坐标：12(4,0),(4,0)AA(3)焦点坐标：12(5,0),(5,0)FFxyO1yx思考：的图像是什么？xy图像无限靠近轴和轴1F2F1A2A(4)离心率:45e5、渐近线1A2A1B2Bxyoxabyxabyab)0,0(12222babyax双曲线.yxab渐近线为：22221,(0,0)xyabab双曲线byxa直线叫做双曲线的渐进线.22143xy的渐进线为：32yx22122xy的渐进线为：yx等轴双曲线2exyObyxabyxa关于x轴、y轴、原点对称图形方程范围对称性顶点离心率22221(0,0)xyababA1(-a,0),A2(a,0)A1(0,-a),A2(0,a)yayaxR或，关于x轴、y轴、原点对称(1)ceea渐进线ayxbxaxayR或，(1)ceeabyxa..yB2A1A2B1xOF2F1F1(-c,0)F2(c,0)xB1yO.F2F1B2A1A2.F2(0,c)F1(0,-c)22221(0,0)yxabab例1.求下列双曲线的渐近线方程，并画出图像：149).122yx149).222yx0xy共轭双曲线22222222(0)0.xyxyabab双曲线渐近线方程02222byax0))((byaxbyax或0byax.0byaxxaby＝能不能直接由双曲线方程推出渐近线方程？结论：100xy(a,b)ab2222双曲线方程中，把1改为0，得oxy例2．已知双曲线的渐近线是，并且双曲线过点02yx)3,4(M求双曲线方程.Q4Moxy练习：已知双曲线渐近线是，并且双曲线过点02yx)5,4(N求双曲线方程.NQ练习题：的双曲线方程。且过点有相同渐近线，求与)3,4(14.222Myx的双曲线方程。且焦点为有相同渐近线，求与)0,5(14.322yx方程。的焦点为顶点的双曲线，且以椭圆求渐近线为1521y.422yxx1.求下列双曲线的渐近线方程：328).122yx819).222yx4).322yx12549).422yx5.双曲线的两条渐近线互相垂直,那么该双曲线的离心率是()A.2B.C.D.12222byax3223226.,10(3,1),,.xyPP已知双曲线关于两坐标轴对称且与圆相交于点若此圆过点的切线与双曲线的一条渐近线平行求此双曲线的方程22918080xyC32.,4.yx如果双曲线的渐近线方程是求双曲线的离心率5543ee或与离心率有关的运算1.双曲线的虚轴长,实轴长,焦距成等差数列,则双曲线的离心率e=____.22223,1,1(0)(1)___________xyaaaa设则双曲线的离心率的取值范围是54(2,5)直线与双曲线的位置关系xyo相交两个公共点相切一个公共点相离无公共点22221xyabykxm方程△>0方程△=0方程△<0复习：直线和椭圆的位置关系A1A2B1B2xyo种类:相离;相切;相交(两个交点,一个交点)位置关系与交点个数相交:两个交点相切:一个交点相离:0个交点相交:一个交点xyoxyo总结两个交点一个交点0个交点相交相离交点个数方程组解的个数相交相切一个交点或两个交点直线和双曲线的位置关系和直线与椭圆的位置关系在分类上是一致的,但在相交是情形不尽相同,椭圆中相交必有两个交点,双曲线中可能有两个,也可能有一个交点.总结例1.判断下列直线与双曲线的位置关系224(3):1,:152516xylyxC相交(一个交点)225(4):...