232平面向量的坐标运算2VIP免费

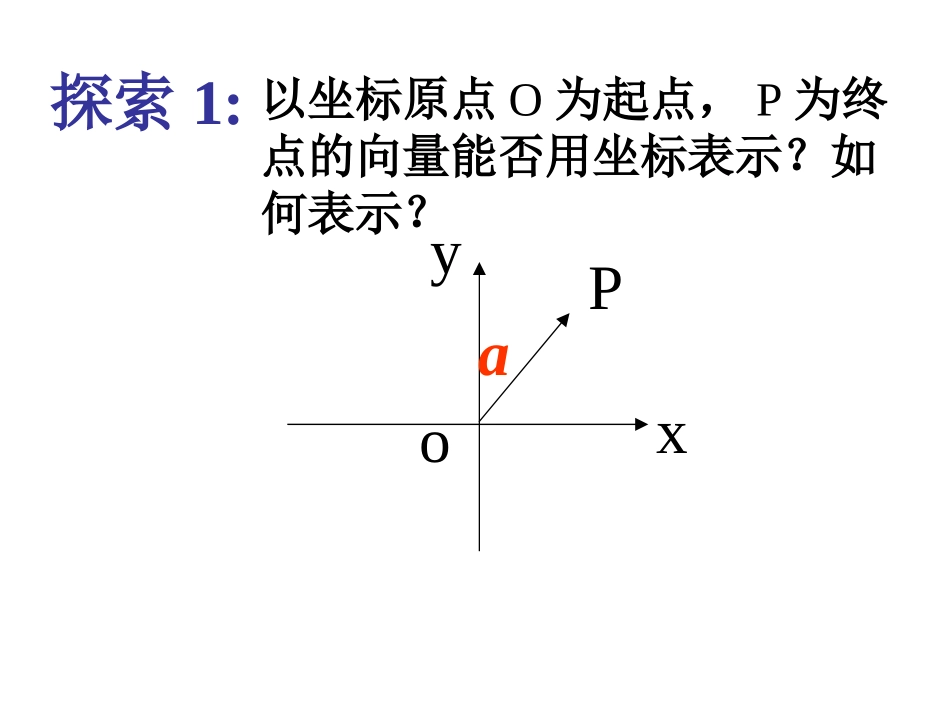
第2章平面向量2.3.2平面向量的坐标运算oxy探索1:以坐标原点O为起点，P为终点的向量能否用坐标表示？如何表示？oPxya4321-1-2-3-2246ij），（yxP(,)OPxiyjxy�向量的坐标表示O向量P（x，y）一一对应OP�xiyj在平面直角坐标系内，起点不在坐标原点O的向量如何用坐标来表示?探索2:oxya在平面直角坐标系内，起点不在坐标原点O的向量如何用坐标来表示?探索2:Aoxyaa可通过向量的平移，将向量的起点移到坐标的原点O处,其终点的坐标（x，y）称为a的（直角）坐标，记a=（x，y）。解决方案:在平面直角坐标系内，若分别取与X轴、Y轴正方向相同的两个单位向量i,j作为基底，任作一向量a，由平面向量基本定理知，有且仅有一对实数x,y,使得a=xi+yj.归纳总结2、单位向量i1、a=xi+yj=(x,y)称其为向量的坐标形式.==(0,0)(0,0)0=（1，0），j=（0，1），对应坐标相等。件是它们的两个向量相等的充要条)2(21212211),(),,(yyxxbayxbyxa则设),(),(),(),(),,(11212121212211yxayyxxbayyxxbayxbyxa则：向量的坐标运算一个重要结论：一个向量的坐标等于表示该向量的终点的坐标减去起点的坐标．说明：），（则向量已知点12122211),,(),,(yyxxAByxByxA),(),(),(12121122yyxxyxyxOAOBABBAx2-x1y2-y1y1y2x2x1yx01（）平面向量的坐标表示1.,aOAxiyjxy��（）OXYA22yxOAa且yx2121(,)ABxxyy�222121||()()ABxxyy�2.若A，B，则11(,)xy22(,)xy的坐标。，，，求向量），，（），，（），，（），，（、如图，已知例CDAOOBOADCBA431431312COYXADB四边形OCDA是平行四边形？例3．已知平行四边形ABCD的三个顶点A、B、C的坐标分别为（－2，1）、（－1，3）、（3，4），求顶点D的坐标．解：设顶点D的坐标为（x，y）），（）），（211321(AB)4,3(yxDC，得由DCAB)4,3()2,1(yxyx423122yx），的坐标为（顶点22D2.如何用坐标表示向量平行(共线)的充要条件?会得到什么样的重要结论?1.向量与非零向量平行(共线)的充要条件是有且只有一个实数,使得abba设即中,至少有一个不为0,则由得),,(11yxa),(22yxbba0,b22,yx01221yxyx01221yxyx这就是说:的充要条件是)0(//bba向量平行的坐标表示3.向量平行(共线)充要条件的两种形式:0)0),,(),,((//)2(;)0(//)1(12212211yxyxbyxbyxabababba1、向量a=(n,1),b=(4,n)共线且方向相同，则n=（）12A.B.±C.2D.±212CC2、平行四边形ABCD的顶点A(-1,-2),B(3,-1),C(5,6),则顶点D的坐标为()A(8,9)B(5,1)C(1,5)D(8,6)课堂练习:2、已知单位正方形ABCD，求的模。,,,ABaBCbACc�23abc53.(3,1),||5,4.(sincos,sincos),ppmm已知且则已知则的长度为110221(21,2),(2,2).,axyxybxyab例题、已知向量为何值时，与共线？相等？与为何值时，又问：bayx,02)2()2()12(yxyx解)2(12yxyxRyx31解得：3131)2(yx解得：210,(3,4)//.ababa例题、已知且，求向量babyxayxa//),4,3(10),,(22又则解：设8686yxyx或解得：0341022yxyx)8,6()8,6(aa或课堂练习:1、已知两点A(0,2)，B(2,0)，则与向量同向量的单位向量是（）AB�22.(,)22A22.(,)22B22.(,)22C22.(,)22DB2、已知a=(1,2),b=(x,1),u=a+2b,v=2a-b且u∥v,求x,1)2(x=3、平面内给定三个向量a=(3,2),b=(-1,2)c=(4,1),回答下列问题:(1)求3a+b-2c;(2)求满足a=mb+nc的实数m,n;(3)若(a+kc)(2∥b-a),求实数k(4)设d=(x,y)满足(d-c)(∥a+b)且|d-c|=1,求d.205525205525(,)(,)5555d或(0,6)58,99mn1613k课后小结2加、减法法则.a+b=(x2,y2)+(x1,y1)=(x2+x1,y2+y1)3向量坐标：若A(x1,y1),B(x2,y2)1向量坐标定义.则=(x2-x1,y2–y1)ABa-b=(x2,y2)-(x1,y1)=(x2-x1,y2-y1)4向量平行的坐标表示：11221221(,),(,),//0axybxyabxyxy若向量则的充要条件是在平面直角坐标系内，我们分别取与X轴、Y轴方向相同的单位向量i,j作为基底，任作一向量a，由平面向量基本定理知，有且仅有一对实数x,y,使得a=xi+yj.向量坐标定义2、把(x,y)叫做向量a的（直角）坐标,记为：a=(x,y),称其为向量的坐标形式.4、其中x、y叫做a在X、Y轴上的坐标.单位向量i=（1，0），j=（0，1）1、把a=xi+yj称为向量基底形式.3、a=xi+yj=(x,y)==(0,0)(0,0)0