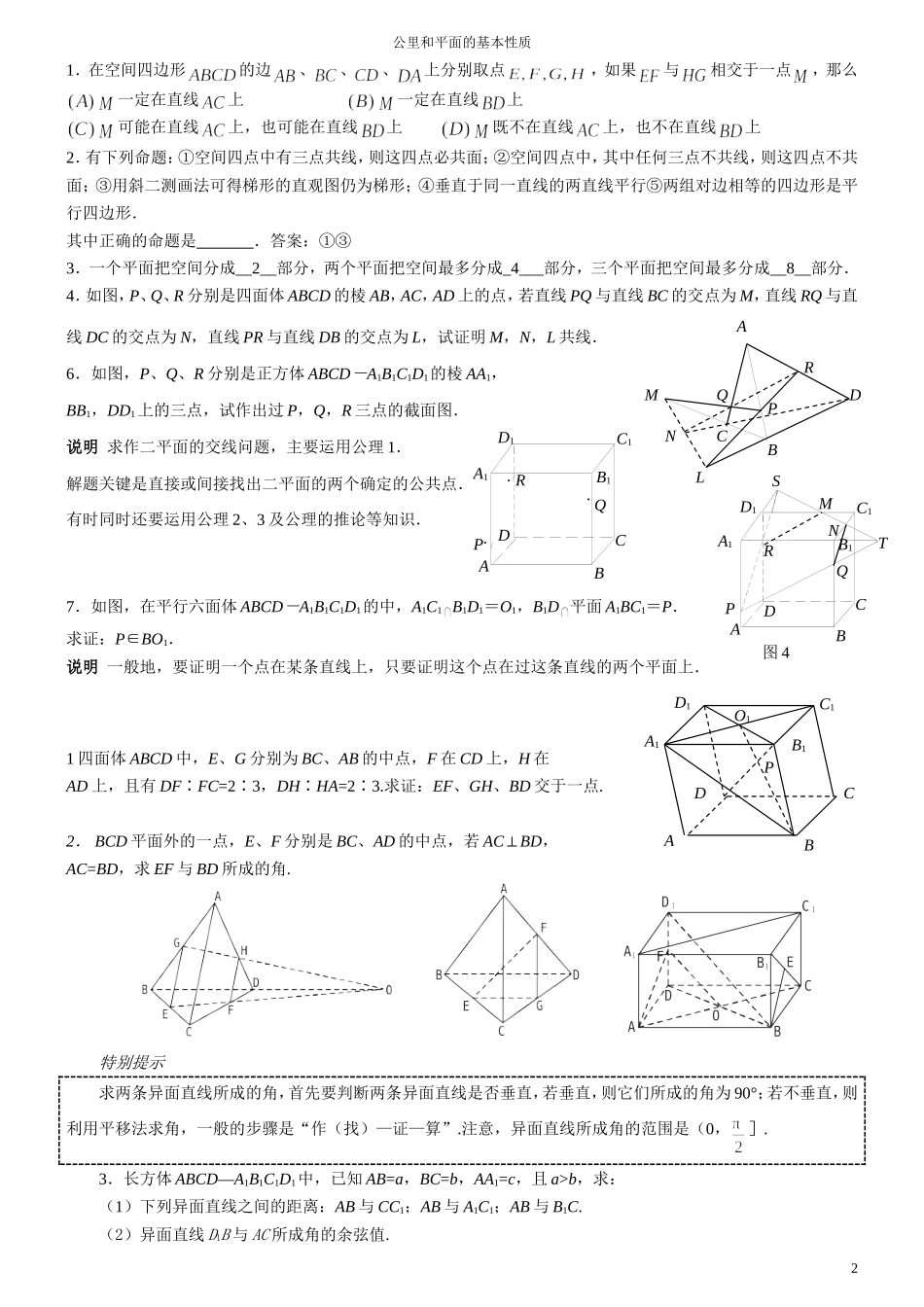
公里和平面的基本性质1.平面的基本性质,即三个公理及推论.2.公理4及等角定理.3.空间两条直线的位置关系有且只有三种,即平行、相交及异面.4.异面直线,求作异面直线所成的角时,往往取题中的特殊点.例1.如图,在四边形ABCD中,已知AB∥CD,直线AB,BC,AD,DC分别与平面α相交于点E,G,H,F.求证:E,F,G,H四点必定共线.说明:在立体几何的问题中,证明若干点共线时,常运用公理2,即先证明这些点都是某二平面的公共点,而后得出这些点都在二平面的交线上的结论.例2.已知:a,b,c,d是不共点且两两相交的四条直线,求证:a,b,c,d共面.说明:证明若干条线(或若干个点)共面的一般步骤是:首先根据公理3或推论,由题给条件中的部分线(或点)确定一个平面,然后再根据公理1证明其余的线(或点)均在这个平面内.本题最容易忽视“三线共点”这一种情况.因此,在分析题意时,应仔细推敲问题中每一句话的含义.例3.如图,点A,B,C确定的平面与点D,E,F确定的平面相交于直线l,且直线AB与l相交于点G,直线EF与l相交于点H,试作出平面ABD与平面CEF的交线.例4.如图,已知平面α,β,且αβ=l.设梯形ABCD中,AD∥BC,且ABα,CDβ,求证:AB,CD,l共点(相交于一点).说明:证明多条直线共点时,一般要应用公理2,这与证明多点共线是一样的.选1.、、表示不同的点,、表示不同的直线,、表示不同的平面,下列推理不正确的是,直线,且不共线与重合2.一个水平放置的平面图形的斜二测直观图是一个底角为,腰和上底边均为1的等腰梯形,则这个平面图形的面积是选3.对于空间三条直线,有下列四个条件:①三条直线两两相交且不共点;②三条直线两两平行;③三条直线共点;④有两条直线平行,第三条直线和这两条直线都相交.其中,使三条直线共面的充分条件有(选)1个2个3个4个4.空间五个点中的任意三点都不共线,由这五个点为顶点只构造出四个三棱锥,则这五个点最多可以确定7个个平面.1αDCBAEFHGE·BAD·FC····E·BAl图3GHD·FCM···αDCBAlβMαbadcGFEAabcdαHK图1图2公里和平面的基本性质1.在空间四边形的边、、、上分别取点,如果与相交于一点,那么一定在直线上一定在直线上可能在直线上,也可能在直线上既不在直线上,也不在直线上2.有下列命题:①空间四点中有三点共线,则这四点必共面;②空间四点中,其中任何三点不共线,则这四点不共面;③用斜二测画法可得梯形的直观图仍为梯形;④垂直于同一直线的两直线平行⑤两组对边相等的四边形是平行四边形.其中正确的命题是.答案:①③3.一个平面把空间分成__2__部分,两个平面把空间最多分成_4___部分,三个平面把空间最多分成__8__部分.4.如图,P、Q、R分别是四面体ABCD的棱AB,AC,AD上的点,若直线PQ与直线BC的交点为M,直线RQ与直线DC的交点为N,直线PR与直线DB的交点为L,试证明M,N,L共线.6.如图,P、Q、R分别是正方体ABCD-A1B1C1D1的棱AA1,BB1,DD1上的三点,试作出过P,Q,R三点的截面图.说明求作二平面的交线问题,主要运用公理1.解题关键是直接或间接找出二平面的两个确定的公共点.有时同时还要运用公理2、3及公理的推论等知识.7.如图,在平行六面体ABCD-A1B1C1D1的中,A1C1B1D1=O1,B1D平面A1BC1=P.求证:P∈BO1.说明一般地,要证明一个点在某条直线上,只要证明这个点在过这条直线的两个平面上.1四面体ABCD中,E、G分别为BC、AB的中点,F在CD上,H在AD上,且有DF∶FC=23∶,DH∶HA=23.∶求证:EF、GH、BD交于一点.2.BCD平面外的一点,E、F分别是BC、AD的中点,若AC⊥BD,AC=BD,求EF与BD所成的角.特别提示求两条异面直线所成的角,首先要判断两条异面直线是否垂直,若垂直,则它们所成的角为90°;若不垂直,则利用平移法求角,一般的步骤是“作(找)—证—算”.注意,异面直线所成角的范围是(0,].3.长方体ABCD—A1B1C1D1中,已知AB=a,BC=b,AA1=c,且a>b,求:(1)下列异面直线之间的距离:AB与CC1;AB与A1C1;AB与B1C.(2)异面直线D1B与AC所成角的余弦值.2A1ABB1DD1CC1RQP···A1ABB1DD1CC1O1PABCDMNLPQRA1ABB1DD1CC1STRQP图4NM