《数学归纳法》VIP免费

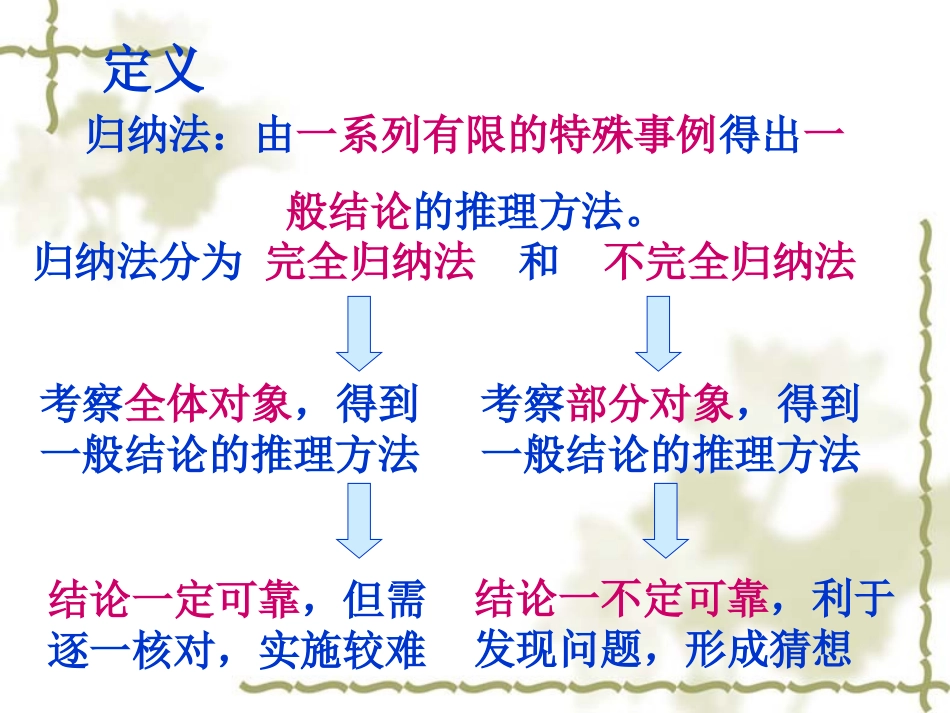
2.32.3数学归纳法数学归纳法（第一课时）（第一课时）问题2：如何证明粉笔盒中的粉笔都是白色的？不完全归纳法完全归纳法情境一问题1:据观察,某天早晨第一个到学校的是女同学,第二个到学校的也是女同学,第三个到学校的还是女同学。于是得出高中的学生全是女同学。归纳法分为完全归纳法和不完全归纳法归纳法：由一系列有限的特殊事例得出一般结论的推理方法。考察全体对象，得到一般结论的推理方法考察部分对象，得到一般结论的推理方法结论一定可靠，但需逐一核对，实施较难结论一不定可靠，利于发现问题，形成猜想定义111a212a313a解:猜想数列的通项公式为717=a515=a616=a818=a919=a•••正整数无限个!414=a引例1：对于数列｛｝，已知，na11=annnaaa+=+11)∈(*Nn（1）求出数列前4项,你能得到什么猜想？（2）猜想一定是正确的吗？怎么证明？)(*Nnnan1有限步骤证明无限对象数学归纳法的感性认识问题4：结合问题1，粉笔盒里的粉笔是有限的，迟早可以拿完，当东西是无穷的时候，那怎么办？首先确定第一次拿出来的是白粉笔，然后再有这样一个保证：当你这一次拿出来的是白粉笔，下一次拿出来的也是白粉笔，在这样的保证下，就可以不费力检查而且做出正确论断“粉笔盒里的粉笔都是白的”，为什么？第一次拿出来的是白粉笔，反复按着保证可得第二次，第三次，……拿出的都是白粉笔。这样用一个推一个的的递推关系使问题得到了解决。如一排排放的很近的自行车，只要碰倒一辆，就会倒下一排，多米诺骨牌游戏，接力比赛，连串鞭炮的燃放，……下面我们重点研究多米诺骨牌游戏，看能否借助其思想方法解决引例的证明问题生活中有许多这种通过“传递”来完成任务的例子游戏游戏11：摆放好多米诺骨牌，推倒第：摆放好多米诺骨牌，推倒第11块骨牌，块骨牌，观察发生的结果？观察发生的结果？第一块要倒下，后面一块接一块倒下游戏游戏22：摆放好多米诺骨牌，推倒第：摆放好多米诺骨牌，推倒第22块骨牌，块骨牌，观察发生的结果？观察发生的结果？这样能使第二块后的所有骨牌都倒下游戏游戏33：摆放好多米诺骨牌，：摆放好多米诺骨牌，推倒第推倒第11块骨牌，块骨牌，第第22块骨牌不倒（第块骨牌不倒（第k+1k+1块骨牌不倒），观察发生的结果？块骨牌不倒），观察发生的结果？问题5：这个游戏中，所有多米诺骨牌全部倒下，必须具备什么条件？（2）任意相邻的两块骨牌，前一块倒下一定导致后一块倒下思考：若把第一、二块骨牌拿走，其它编号的骨牌不变，若让第三块骨牌倒下，第二个条件不变情况会怎么样？请谈谈为什么只要满足上述两个条件，所有多米诺骨牌就能全部倒下？（1）第一块骨牌倒下；多米诺骨牌游戏的原理这个猜想的证明方法1nan（1）第一块骨牌倒下。（2）若第k块倒下时，则相邻的第k+1块也倒下。根据（1）和（2），可知不论有多少块骨牌，都能全部倒下。（1）当n=1时猜想成立。（2）若当n=k时猜想成立，即，则当n=k+1时猜想也成立，即。1kak111kak根据（1）和（2），可知对任意的正整数n，猜想都成立。类比多米诺骨牌游戏,证明引例猜想成立由此，你认为证明一个与正整数有关的命题，可以按怎样的步骤进行？n数学归纳法定义一般地，证明一个与正整数n有关的命题步骤：根据（1）和（2），可知命题从n0开始的所有正整数n都成立。这种证明方法叫做数学归纳法（2）归纳递推:假设当n=k(k∈N*,k≥时命题成立,证明当n=k+1时命题也成立。*0Nn(1)(归纳奠基)证明当n取第一个值（）时命题成立。0n0n为什么完成了“两个步骤和一个结论”就说明命题对所有的正整数都成立？思维过程当时命题成立，可以推出时命题成立，当时命题成立，可以推出当时命题成立…)(*0Nnnk)(1*0Nnnk)(1*0Nnnk)(2*0Nnnk理解定义：利用命题自身具有的传递性，实现无穷三段论的循环论证。用有限的步骤，来论证无限结论。数学归纳法特点：数学归纳法应用一：证明等式证明：（1）当n=1时，左边=12=1右边=1等式成立(2)假设当n=k时等式成立,即6)12)(1(3212222++=+•••+++kkkk那么,当n=k+1时2)1(++k6)1(6)12)(1(2++++=kkkk6)672)(1(2+++=kkk6)32)(2)(1(+++=kkk6]1)1(2][1)1)[(1(+++++=...