必修二232《平面与平面垂直的判定》课件（共19张PPT）VIP免费

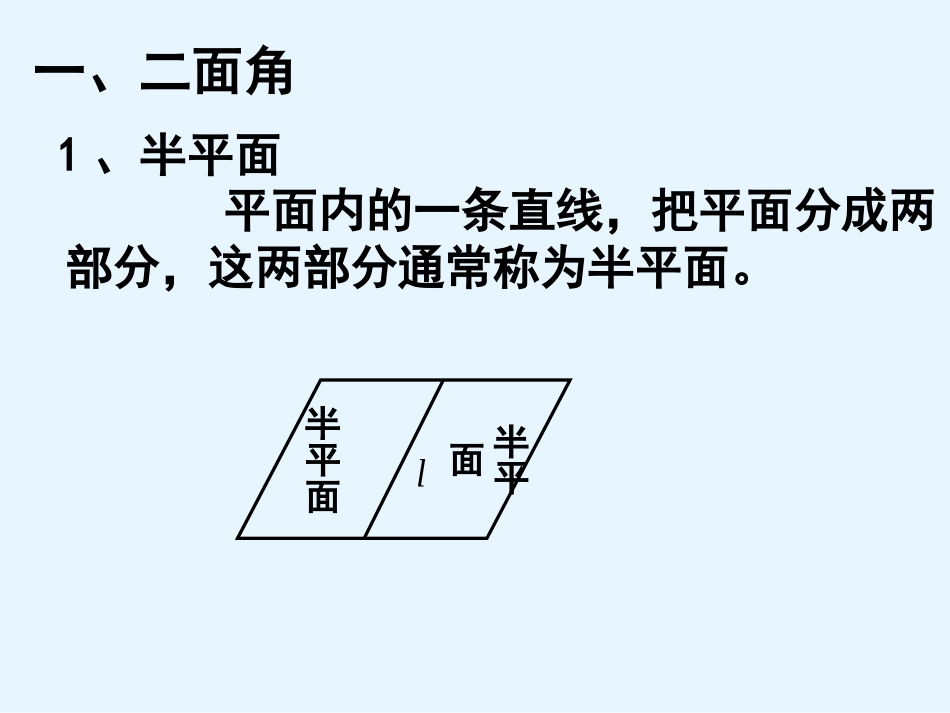
南漳二中魏品强请观察滑梯面与地面构成的图形平面内的一条直线，把平面分成两部分，这两部分通常称为半平面。1、半平面一、二面角l半平面半平面2、二面角从一条直线出发的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱，这两个半平面叫做二面角的面。lABlABPQAB记作：二面角l记作：二面角lQ记作：二面角PABQ记作：二面角P在二面角的棱上任取一点O，以点O为垂足，在两个半平面内分别作垂直于棱的射线OA,OB，则射线OA和OB构成的角叫做二面角的平面角。lOABAOB二、二面角的平面角OOABABAOB==BOA?l例1：在所有棱长都相等的三棱锥A-BCD中，找出二面角A-CD-B的平面角。两个平面相交,如果它们所成的二面角是直二面角，就说这两个平面相互垂直.记作:三、两个平面互相垂直（把直立平面的竖边画成与水平平面的横边垂直）问题：如何检测所砌的墙面和地面是否垂直？问题：如何检测所砌的墙面和地面是否垂直？一个平面过另一个平面的垂线，则这两个平面垂直.关键：找平面的垂线四、两个平面垂直的判定定理例1如果一个平面经过了另一个平面的一条垂线，那么这两个平面互相垂直。已知：ABβ⊥，ABα求证：αβ.⊥∪证明：αβCDABE在平面β内过B点作直线BECD⊥，则∠ABE就是二面角α--CD--β的平面角，设α∩β=CD,则BCD.∈∪∵ABβ⊥，CDβ，∴ABCD.⊥∪∵ABβ⊥，BEβ，∴ABBE.⊥∴二面角α--CD--β是直二面角，∴αβ.⊥αβCDABE例2:如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A,B的任意一点，求证：PACPBC.平面平面PABCO你还能发现哪些平面互相垂直？为什么？练习1：AB⊥平面BCD,BCCD⊥问：(1)图中哪些面互相垂直,为什么？(2)图中有几个直角三角形？并证明之.ABCD答案：四个面都是直角三角形练习2：如图所示，四边形ABCD是平行四边形，直线SC⊥平面ABCD，E是SA的中点，求证：平面EDB⊥平面ABCD．ABCDESABCDA1B1C1D1练习3:在正方体ABCD－A1B1C1D1中，求证：111ACCAABD平面平面变式:（1）找出二面角A-BD-A1的平面角；（2）求二面角B-CC1-A1的大小.∠AOA145°归纳小结：(2)判定面面垂直的两种方法：①定义法②根据面面垂直的判定定理(3)从面面垂直的判定定理我们还可以看出面面垂直的问题可以转化为线面垂直的问题来解决.（转化思想）(1)二面角及其二面角的平面角作业：P73A组3、4