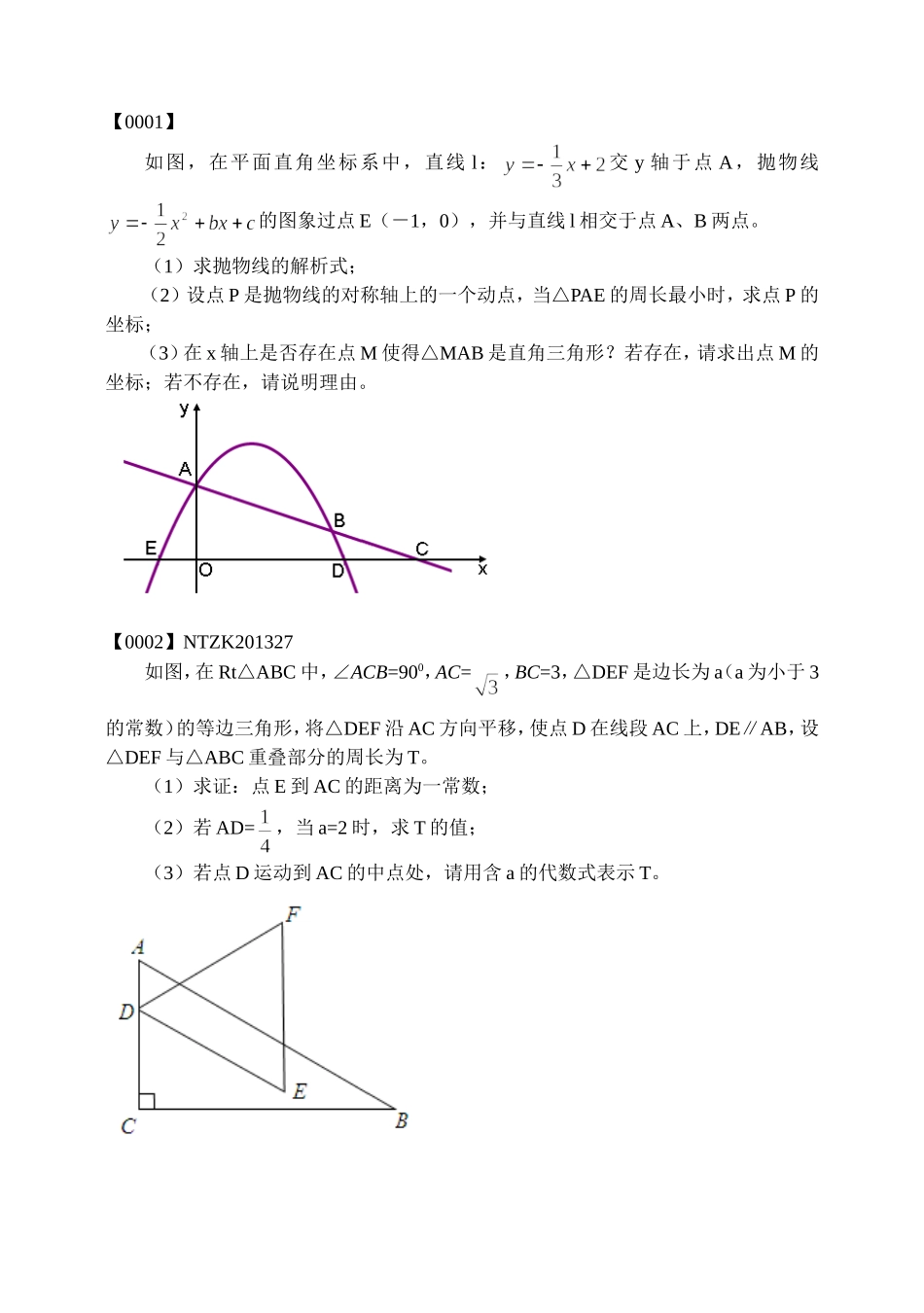
【0001】如图,在平面直角坐标系中,直线l:交y轴于点A,抛物线的图象过点E(-1,0),并与直线l相交于点A、B两点。(1)求抛物线的解析式;(2)设点P是抛物线的对称轴上的一个动点,当△PAE的周长最小时,求点P的坐标;(3)在x轴上是否存在点M使得△MAB是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由。【0002】NTZK201327如图,在Rt△ABC中,∠ACB=900,AC=,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。(1)求证:点E到AC的距离为一常数;(2)若AD=,当a=2时,求T的值;(3)若点D运动到AC的中点处,请用含a的代数式表示T。【0003】NTZK201328如图,直线(b>0)与抛物线相交于A,B两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且(1)求b的值;(2)求证:点在反比例函数的图象上;(3)求证:。【0004】NTZK201227如图,在△ABC中,AB=AC=10cm,BC=12cm,点D是BC边的中点.点P从点B出发,以acm/s(a>0)的速度沿BA匀速向点A运动;点Q同时以1cm/s的速度从点D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为ts.(1)若a=2,△BPQ∽△BDA,求t的值;(2)设点M在AC上,四边形PQCM为平行四边形.①若a=,求PQ的长;②是否存在实数a,使得点P在∠ACB的平分线上?若存在,请求出a的值;若不存在,请说明理由.【0005】NTZK201228如图,经过点A(0,-4)的抛物线y=+bx+c与x轴相交于点B(-2,0)和C,O为坐标原点.(1)求抛物线的解析式;(2)将抛物线y=+bx+c向上平移个单位长度、再向左平移m(m>0)个单位长度,得到新抛物线.若新抛物线的顶点P在△ABC内,求m的取值范围;(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,求AM的长.【0006】NTZK201127已知A(1,0)、B(0,-1)、C(-1,2)、D(2,-1)、E(4,2)五个点,抛物线(a>0)经过其中的三个点。(1)求证:C、E两点不可能同时在抛物线(a>0)上;(2)点A在抛物线(a>0)上吗?为什么?(3)求a和k的值.【0007】NTZK201128如图,已知直线l经过点A(1,0),与双曲线y=(x>0)交于点B(2,1).过点P(p,p-1)(p>1)作x轴的平行线分别交双曲线y=(x>0)和y=-(x<0)于点M、N.(1)求m的值和直线l的解析式;(2)若点P在直线y=2上,求证:△PMB∽△PNA;(3)是否存在实数p,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.【0008】NTZK201027如图,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连结DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.(1)求y关于x的函数关系式;(2)若m=8,求x为何值时,y的值最大,最大值是多少?(3)若,要使△DEF为等腰三角形,m的值应为多少?【0009】NTZK201028已知抛物线经过A(-4,3)、B(2,0)两点,当x=3和x=-3时,这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与x轴平行,O为坐标原点。(1)求直线AB和这条抛物线的解析式;(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明理由;(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线上的动点,当△PDO的周长最小时,求四边形CODP的面积。【0011】NTZK201027已知二次函数的图像如图。(1)求它的对称轴与轴交点D的坐标;(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与轴,轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由。【0010】在直角坐标系xoy中,已知点P是反比例函数图像上一个动点,以P为圆心的圆始终与y轴相切,设切点为A(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由。(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:①求过A,B,C三点的抛物线的解析式。②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的,若存在...