空间立体几何(教师)VIP免费

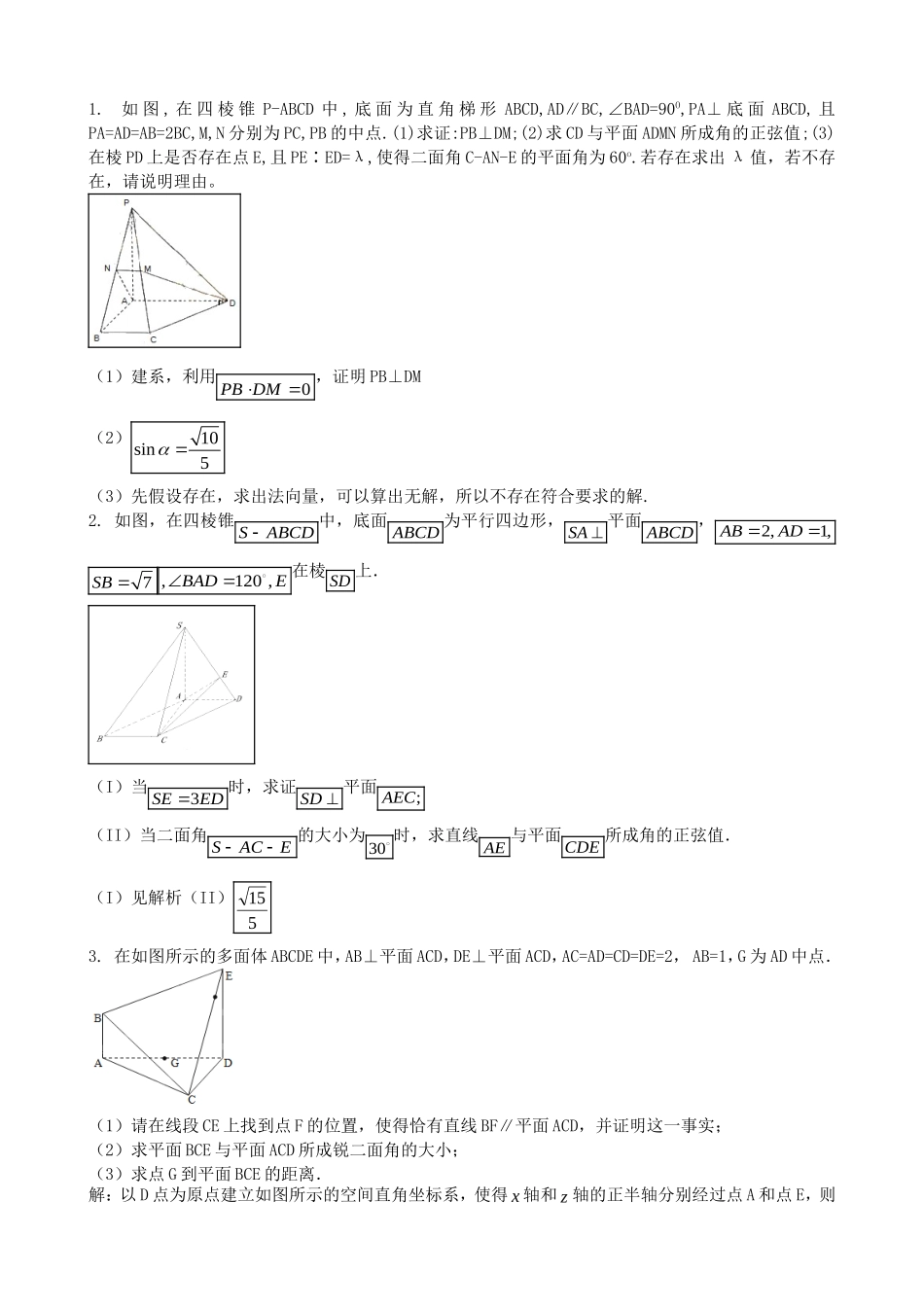
1.如图,在四棱锥P-ABCD中,底面为直角梯形ABCD,AD∥BC,∠BAD=90O,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.(1)求证:PB⊥DM;(2)求CD与平面ADMN所成角的正弦值;(3)在棱PD上是否存在点E,且PE∶ED=λ,使得二面角C-AN-E的平面角为60o.若存在求出λ值，若不存在，请说明理由。（1）建系，利用0PBDM�，证明PB⊥DM（2）10sin5（3）先假设存在，求出法向量，可以算出无解，所以不存在符合要求的解.2.如图，在四棱锥SABCD中，底面ABCD为平行四边形，SA平面ABCD，2,1,ABAD7SB,120,BADE在棱SD上．（I）当3SEED时，求证SD平面;AEC（II）当二面角SACE的大小为30时，求直线AE与平面CDE所成角的正弦值．（I）见解析（II）5153.在如图所示的多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2，AB=1，G为AD中点．（1）请在线段CE上找到点F的位置，使得恰有直线BF∥平面ACD，并证明这一事实；（2）求平面BCE与平面ACD所成锐二面角的大小；（3）求点G到平面BCE的距离．解：以D点为原点建立如图所示的空间直角坐标系，使得x轴和z轴的正半轴分别经过点A和点E，则各点的坐标为(0,0,0)D，(2,0,0)A，(0,0,2)E，(2,0,1)B，(1,3,0)C，（1）点F应是线段CE的中点，下面证明：设F是线段CE的中点，则点F的坐标为13(,,1)22F，∴33(,,0)22BF�，显然BF�与平面xOy平行，此即证得BF∥平面ACD；（2）设平面BCE的法向量为(,,)nxyz，则nCB��，且nCE��，由(1,3,1)CB�，(1,3,2)CE�，∴30320xyzxyz，不妨设3y，则12xz，即(1,3,2)n，∴所求角满足(0,0,1)2cos2||nn，∴4；（3）由已知G点坐标为（1，0，0），∴(1,0,1)BG�，由（2）平面BCE的法向量为(1,3,2)n，∴所求距离3||24||BGndn�．4.如图，四棱锥P-ABCD的底面ABCD是矩形，侧面PAB是正三角形，AB=2，BC=2，PC=6，（I）求证：PD⊥AC；（II）已知棱PA上有一点E，若二面角E—BD—A的大小为45°，试求BP与平面EBD所成角的正弦值。BADCGFEzxy5.如图,在三棱拄111ABCABC中,AB侧面11BBCC,已知11,3BCBCC(Ⅰ)求证:1CBABC平面;(Ⅱ)试在棱1CC(不包含端点1,)CC上确定一点E的位置,使得1EAEB;(Ⅲ)在(Ⅱ)的条件下,若求二面角11AEBA的平面角的正切值.EC1B1A1CBA证(Ⅰ)因为AB侧面11BBCC,故1ABBC在1BCC中,1111,2,3BCCCBBBCC由余弦定理有2211112cos1422cos33BCBCCCBCCCBCCEC1B1A1CBA故有222111BCBCCCCBBC而BCABB且,ABBC平面ABC1CBABC平面(Ⅱ)由11,,,,EAEBABEBABAEAABAEABE平面从而1BEABE平面且BEABE平面故1BEBE不妨设CEx,则12CEx,则221BExxzyxEC1B1A1CBA又1123BCC则2211BExx在1RtBEB中有22114xxxx从而1x(舍负)故E为1CC的中点时,1EAEB法二:以B为原点1,,BCBCBA�为,,xyz轴,设CEx,则11(0,0,0),(1),(1,3,0),(0,0,2)2BExBA由1EAEB得10EAEB�即1313(1,,2)(2,3,0)022221133(1)(2)302222xxxxxxxx化简整理得2320xx1x或2x当2x时E与1C重合不满足题意当1x时E为1CC的中点故E为1CC的中点使1EAEB(Ⅲ)取1EB的中点D,1AE的中点F,1BB的中点N,1AB的中点M连DF则11//DFAB,连DN则//DNBE,连MN则11//MNAB连MF则//MFBE,且MNDF为矩形,//MDAE又1111,ABEBBEEB故MDF为所求二面角的平面角NMFDEC1B1A1CBA在RtDFM中,1112(22DFABBCE为正三角形）111222MFBECE122tan222MDF法二:由已知1111,EAEBBAEB�,所以二面角11AEBA的平面角的大小为向量11BA�与EA�的夹角因为11(0,0,2)BABA�31(,,2)22EA�故111122costan23EABAEABA��6.如图,三棱柱111ABCABC的侧棱1AA底面ABC,90ACB,E是棱1CC上动点,F是AB的中点,11,2,4ACBCAA(Ⅰ)当E是1CC中点时,求证:CF∥平面1AEB;(Ⅱ)在棱1CC上是否存在点E,使得二面角1AEBB的余弦值是21717...