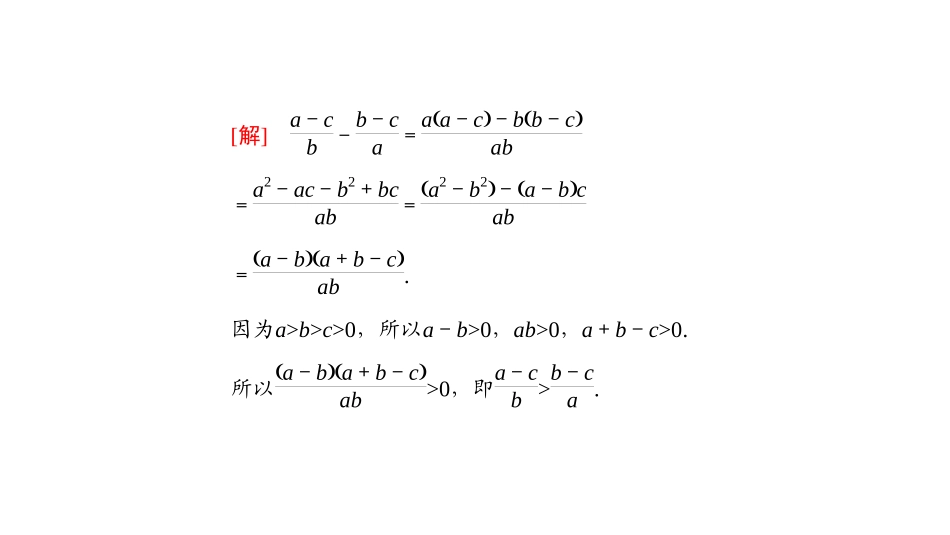作差法与作商法比较大小VIP免费

类型二利用作差法比较大小[例2]已知a>b>c>0，试比较a－cb与b－ca的大小．[解]a－cb－b－ca＝aa－c－bb－cab＝a2－ac－b2＋bcab＝a2－b2－a－bcab＝a－ba＋b－cab.因为a>b>c>0，所以a－b>0，ab>0，a＋b－c>0.所以a－ba＋b－cab>0，即a－cb>b－ca.[点评]本题采用“作差法”比较两个代数式的大小，关键是作差变形后能准确地判断符号．判断符号要注意配方、因式分解、有理化、通分等方法的灵活使用．“作差法”的一般步骤：①作差；②变形；③判断符号；④得出结论．变式训练2已知a>0，试比较a与1a的大小．解：∵a－1a＝a2－1a＝a－1a＋1a，∵a>0，∴当a>1时，a－1a＋1a>0，有a>1a；当a＝1时，a－1a＋1a＝0，有a＝1a；当01时，a>1a；当a＝1时，a＝1a；当00∴2x2+3x+5>5x2+3x+2=6x2+3x+5–5x2-3x-2=x2+3•解：6x2+3x+5–(5x2+3x+2)把整体看着实数轴上的一个a把整体看着实数轴上的一个b作差整理变形定号下结论类型三利用作商法比较大小[例3]设a>0，b>0，且a≠b，比较aabb与abba的大小．[分析]因为a>0，b>0，所以我们只要比较aabbabba与1的大小即可．[解]aabbabba＝aa－b·bb－a＝(ab)a－b，当a>b>0时，ab>1，且a－b>0，∴(ab)a－b>1.即aabb>abba；当b>a>0时，01.即aabb>abba.综上知：aabb>abba.变式训练3若a>0，比较aa与3a的大小．解：aa3a＝(a3)a当03时，a3>1，(a3)a>1，aa>3a.1．设M＝x2，N＝x－1，则M与N的大小关系为()A．M>NB．M＝NC．M0∴M>N答案：M>N