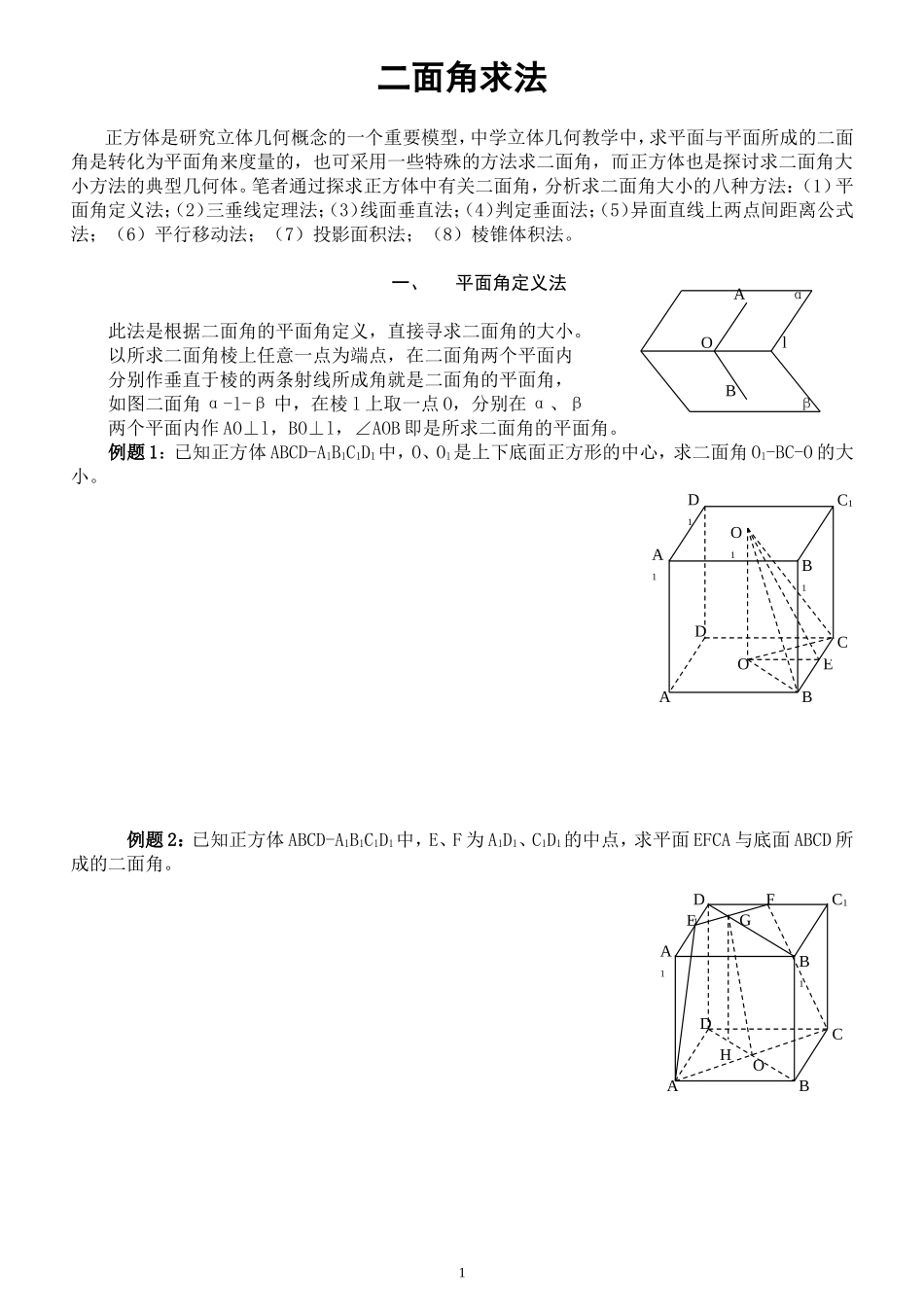
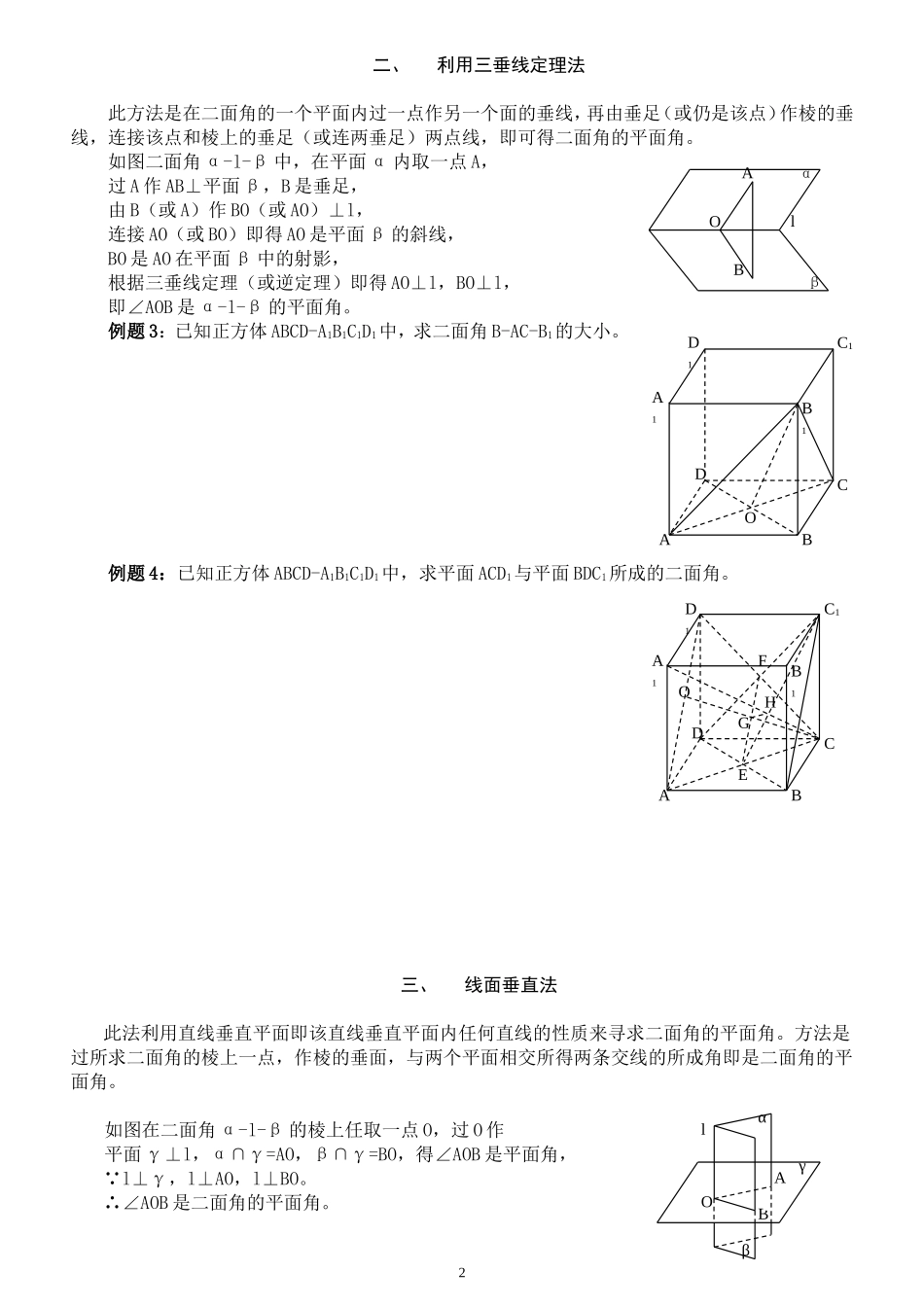
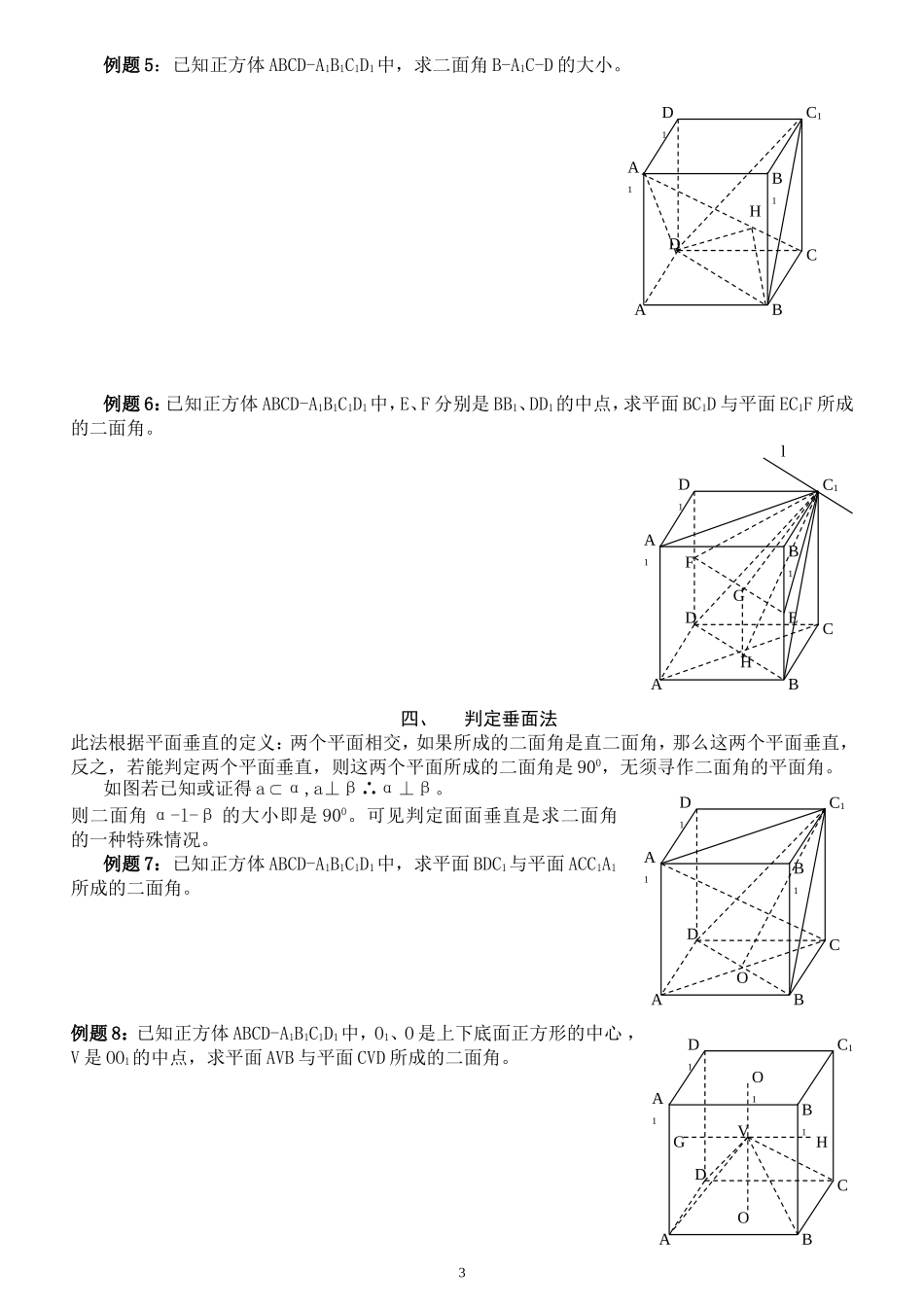
二面角求法正方体是研究立体几何概念的一个重要模型,中学立体几何教学中,求平面与平面所成的二面角是转化为平面角来度量的,也可采用一些特殊的方法求二面角,而正方体也是探讨求二面角大小方法的典型几何体。笔者通过探求正方体中有关二面角,分析求二面角大小的八种方法:(1)平面角定义法;(2)三垂线定理法;(3)线面垂直法;(4)判定垂面法;(5)异面直线上两点间距离公式法;(6)平行移动法;(7)投影面积法;(8)棱锥体积法。一、平面角定义法此法是根据二面角的平面角定义,直接寻求二面角的大小。以所求二面角棱上任意一点为端点,在二面角两个平面内分别作垂直于棱的两条射线所成角就是二面角的平面角,如图二面角α-l-β中,在棱l上取一点O,分别在α、β两个平面内作AO⊥l,BO⊥l,∠AOB即是所求二面角的平面角。例题1:已知正方体ABCD-A1B1C1D1中,O、O1是上下底面正方形的中心,求二面角O1-BC-O的大小。例题2:已知正方体ABCD-A1B1C1D1中,E、F为A1D1、C1D1的中点,求平面EFCA与底面ABCD所成的二面角。1BAOlβαHOGFEADD1C1B1A1CBO1OEADD1C1B1A1CB二、利用三垂线定理法此方法是在二面角的一个平面内过一点作另一个面的垂线,再由垂足(或仍是该点)作棱的垂线,连接该点和棱上的垂足(或连两垂足)两点线,即可得二面角的平面角。如图二面角α-l-β中,在平面α内取一点A,过A作AB⊥平面β,B是垂足,由B(或A)作BO(或AO)⊥l,连接AO(或BO)即得AO是平面β的斜线,BO是AO在平面β中的射影,根据三垂线定理(或逆定理)即得AO⊥l,BO⊥l,即∠AOB是α-l-β的平面角。例题3:已知正方体ABCD-A1B1C1D1中,求二面角B-AC-B1的大小。例题4:已知正方体ABCD-A1B1C1D1中,求平面ACD1与平面BDC1所成的二面角。三、线面垂直法此法利用直线垂直平面即该直线垂直平面内任何直线的性质来寻求二面角的平面角。方法是过所求二面角的棱上一点,作棱的垂面,与两个平面相交所得两条交线的所成角即是二面角的平面角。如图在二面角α-l-β的棱上任取一点O,过O作平面γ⊥l,α∩γ=AO,β∩γ=BO,得∠AOB是平面角, l⊥γ,l⊥AO,l⊥BO。∴∠AOB是二面角的平面角。2BAOlβαOADD1C1B1A1CBlBAγβαOHGFOEADD1C1B1A1CB例题5:已知正方体ABCD-A1B1C1D1中,求二面角B-A1C-D的大小。例题6:已知正方体ABCD-A1B1C1D1中,E、F分别是BB1、DD1的中点,求平面BC1D与平面EC1F所成的二面角。四、判定垂面法此法根据平面垂直的定义:两个平面相交,如果所成的二面角是直二面角,那么这两个平面垂直,反之,若能判定两个平面垂直,则这两个平面所成的二面角是900,无须寻作二面角的平面角。如图若已知或证得aα,a⊥β∴α⊥β。则二面角α-l-β的大小即是900。可见判定面面垂直是求二面角的一种特殊情况。例题7:已知正方体ABCD-A1B1C1D1中,求平面BDC1与平面ACC1A1所成的二面角。例题8:已知正方体ABCD-A1B1C1D1中,O1、O是上下底面正方形的中心,V是OO1的中点,求平面AVB与平面CVD所成的二面角。3OADD1C1B1A1CBVOO1HGADD1C1B1A1CBHADD1C1B1A1CBlGEFHADD1C1B1A1CB五、异面直线上两点间距离公式法此法按高中立体几何课本P45页例2证明的公式,求二面角大小,题意是已知两条异面直线a、b上分别取点E、F,设A’E=m,AF=n,求EF。如图公式是:EF=(注意E、F在AA1同侧时取“-”,EF在AA1异侧时取“+”号。)应用该公式是求异面直线上两点间的距离,若把所求二面角当作θ角,即是异面直线a、b和公垂线AA1确定的两个平面所成的二面角,用函数观念来理解公式中五个量,已知其中四个量即可求第五个量,若已知或易求知EF、d、m、n则求cosθ,θ即是所求二面角。例题9:已知正方体ABCD-A1B1C1D1中,H是BC棱上一点且BH:BC=1:3,求二面角H-AA1-C1的大小。例题10:已知正方体ABCD-A1B1C1D1中,O1、O是上下底面正方形的中心,E是AB棱上一点,且AE:EB=1:2,求二面角A1-O1O-E的大小。六、平行移动法若所求二面角的棱线隐含未知或难寻作棱时,可采用将二面角中的一个平面平行移动到适当位置,作得新的二面角大小与所求二面角相等,并可求得新的二面角大小。如图将所求平面α与平面β所成的二面角中...