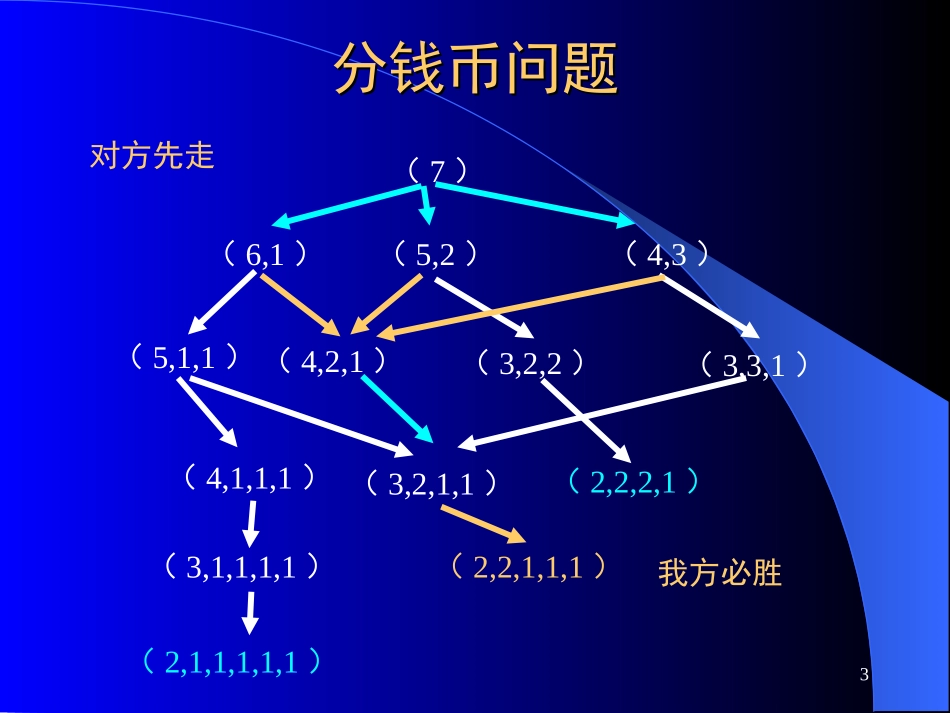
第二章对抗搜索第二章对抗搜索对抗搜索:博弈博弈问题极小极大方法-剪枝蒙特卡洛博弈方法122.12.1博弈问题博弈问题博弈问题–双人–一人一步–双方信息完备–零和3分钱币问题分钱币问题(7)(6,1)(5,2)(4,3)(5,1,1)(4,2,1)(3,2,2)(3,3,1)(4,1,1,1)(3,2,1,1)(2,2,2,1)(3,1,1,1,1)(2,2,1,1,1)(2,1,1,1,1,1)对方先走我方必胜4中国象棋中国象棋一盘棋平均走50步,总状态数约为10的161次方。假设1毫微秒走一步,约需10的145次方年。结论:不可能穷举。502.22.2极小极大过程极小极大过程5-333-3022-30-23541-30689-30-33-3-3-21-36-30316011极大极小ab0262.32.3--剪枝剪枝极大节点的下界为。极小节点的上界为。剪枝的条件:–后辈节点的值≤祖先节点的值时,剪枝–后辈节点的值≥祖先节点的值时,剪枝简记为:–极小≤极大,剪枝–极大≥极小,剪枝7486-315035--剪枝(续)剪枝(续)-33-3022-30-2309-300-303305411-31661abcdefghijkmn2.42.4蒙特卡洛博弈方法蒙特卡洛博弈方法为什么-剪枝方法在围棋上失效?-剪枝方法存在的问题依赖于局面评估的准确性–局面评估问题大量专家知识知识的统一性问题人工整理8围棋落子模型围棋落子模型围棋对弈过程可以看做一个马尔科夫过程:五元组:{T,S,A(i),P(·|i,a),r(i,a)}–T:决策时刻–S:状态空间,S={i}–A(i):可行动集合(可落子点)–P(·|i,a):状态i下选择行动a的概率–r(i,a):状态i下选择行动a后课获得的收益9蒙特卡洛方法蒙特卡洛方法二十世纪40年代中期S.M.乌拉姆和J.冯·诺伊曼提出的一种随机模拟方法–多重积分–矩阵求逆–线性方程组求解–积分方程求解–偏微分方程求解–随机性问题模拟10蒲丰投针问题蒲丰投针问题1777年法国科学家蒲丰提出一种计算π的方法:取一张白纸,在上面画上许多条间距为d的等距平行线,另取一根长度为l(l