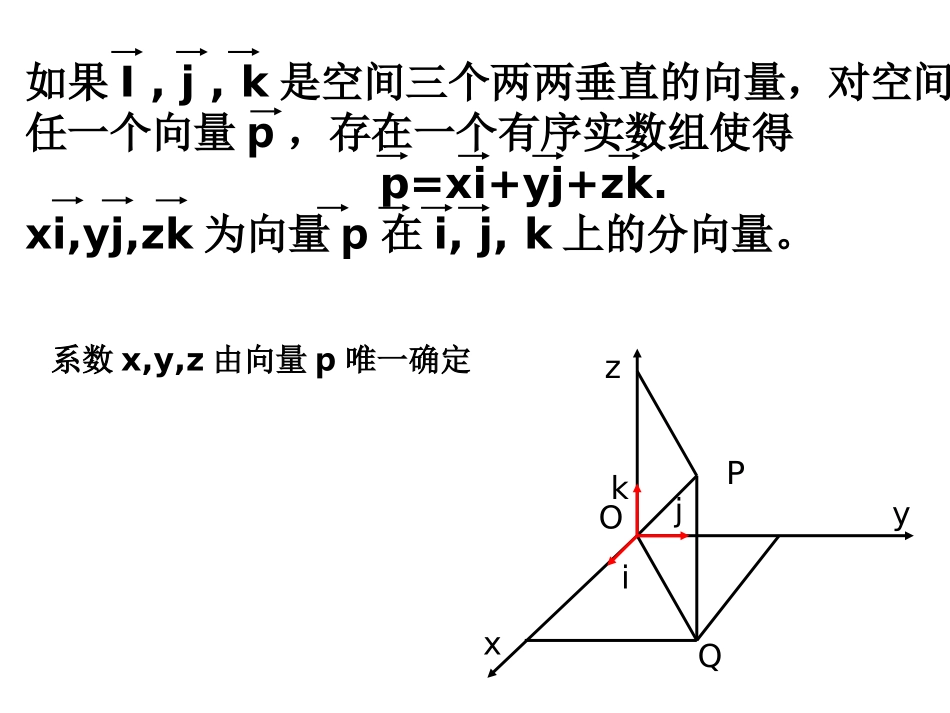
3.2.空间向量的坐标xyzkijQPO一、空间向量基本定理:如图,设i,j,k是空间三个两两垂直的向量,且有公共起点O。对于空间任意一个向量p=OP,设点Q为点P在i,j所确定的平面上的正投影,由平面基本定理可知,在O,Q,k所确定的平面上,存在实数z,使得OP=OQ+zk,而在i,j所确定的平面上,由平面向量基本定理可知,存在有序之前数对(x,y),使得OQ=xi+yj.从而OP=OQ+zk=xi+yj+zk.xyzkijQPO如果I,j,k是空间三个两两垂直的向量,对空间任一个向量p,存在一个有序实数组使得p=xi+yj+zk.xi,yj,zk为向量p在i,j,k上的分向量。系数x,y,z由向量p唯一确定思考:在空间中,如果用任意三个不共面向量a,b,c代替两两垂直的向量i,j,k,能得到类似的结论吗?空间向量基本定理:如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc.空间所有向量的集合{p|p=xa+yb+zc,x,y,z∈R}{a,b,c}叫做空间的一个基底,a,b,c都叫做基向量。二、空间直角坐标系单位正交基底:如果空间的组个基底的三个基向量互相垂直,且长都为1,则这组基底叫做单位正交基底,常用i,j,k表示空间直角坐标系:在空间选定一点O和一组单位正交基底i、j、k。以点O为原点,分别以i、j、k的正方向建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这样就建立了一个空间直角坐标系O--xyz点O叫做原点,向量I、j、k都叫做坐标向量.通过每两个坐标轴的平面叫做坐标平面。在空间直角坐标系O--xyz中,对空间任一点,A,对应一个向量OA,于是存在唯一的有序实数组x,y,z,使OA=xi+yj+zk在单位正交基底i,j,k中与向量OA对应的有序实数组(x,y,z),叫做点A在此空间直角坐标系中的坐标,记作A(x,y,z),其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标.三、向量的直角坐标运算.111222(,,),(,,)axyzbxyz设则121212(,,);abxxyyzz121212(,,);abxxyyzz111(,,)();axyzR121212;abxxyyzz121212//,,()abxxyyzzR1212120.abxxyyzz设A(x1,y1,z1),B(x2,y2,z2),则AB=OB-OA=(x2,,y2,z2)-(x1,y1,z1)=(x2-x1,y2-y1,z2-z1).一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标.空间向量坐标运算法则,关键是注意空间几何关系与向量坐标关系的转化,为此在利用向量的坐标运算判断空间几何关系时,首先要选定单位正交基,进而确定各向量的坐标。二、距离与夹角2222111||aaaxyz2222222||bbbxyz1.距离公式(1)向量的长度(模)公式注意:此公式的几何意义是表示长方体的对角线的长度。||��ABABABAB212121(,,)xxyyzz222212121()()()xxyyzz222,212121()()()ABdxxyyzz在空间直角坐标系中,已知、,则111(,,)Axyz222(,,)Bxyz(2)空间两点间的距离公式终点坐标减起点坐标cos,||||ababab112233222222123123;abababaaabbb2.两个向量夹角公式注意:(1)当时,同向;(2)当时,反向;(3)当时,。cos,1ab与abcos,1ab与abcos,0abab思考:当及时,的夹角在什么范围内?1cos,0ab,10cosab三、应用举例例1已知、,求:(1)线段的中点坐标和长度;(3,3,1)A(1,0,5)BAB解:设是的中点,则(,,)MxyzAB113()(3,3,1)1,0,52,,3,222�OMOAOB∴点的坐标是.M32,,32222,(13)(03)(51)29.ABdOABM(2)到两点距离相等的点的坐标满足的条件。、AB(,,)Pxyz,,xyz解:点到的距离相等,则(,,)Pxyz、AB222222(3)(3)(1)(1)(0)(5),xyzxyz化简整理,得46870xyz即到两点距离相等的点的坐标满足的条件是、AB(,,)xyz46870xyz例2如图,在正方体中,,求与所成的角的余弦值。1111ABCDABCD11BE11114ABDF1BE1DFF1E1C1B1A1D1DABCyzxO解:设正方体的棱...