面面垂直的判定和性质定理VIP免费

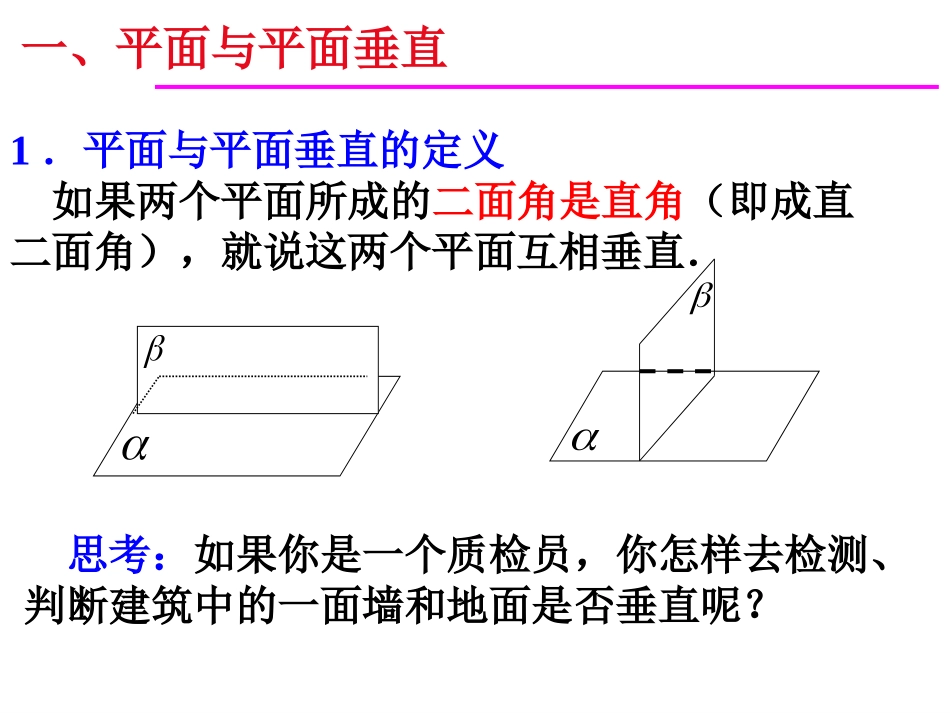
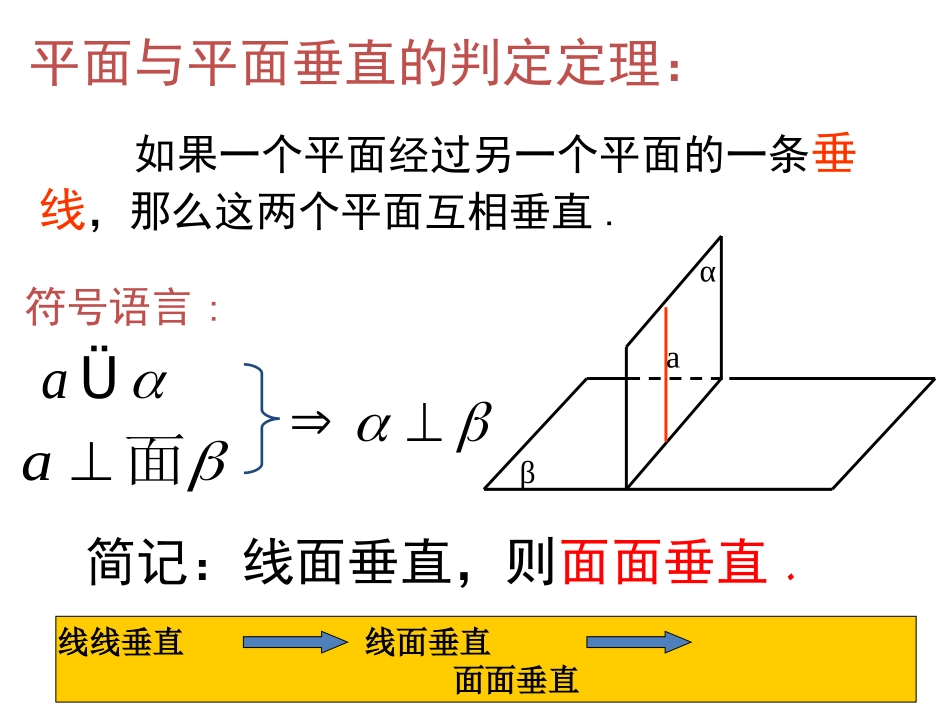
平面与平面的垂直关系一、平面与平面垂直1．平面与平面垂直的定义如果两个平面所成的二面角是直角（即成直二面角），就说这两个平面互相垂直．思考：如果你是一个质检员，你怎样去检测、判断建筑中的一面墙和地面是否垂直呢？平面与平面垂直的判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直.αβa简记：线面垂直，则面面垂直.面面垂直线面垂直线线垂直aÜa面符号语言:如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直．已知：AB⊥β，ABα（图1）．求证：α⊥β。 ABβ⊥，CDβ，两个平面垂直的判定定理证明：设α∩β=CD，∴ABCD⊥．在平面β内过点B作直线BECD⊥，则∠ABE是二面角α-CD-β的平面角，而ABBE⊥，故α-CD-β是直二面角．∴αβ⊥。探究1：ACBDA1C1B1D111AABBABCD面面CCBBBBAA1111面面111111DCBABBAA面面DDAABBAA1111面面面面垂直线面垂直线线垂直如图为正方体,请问哪些平面与面垂直?11AABB,,ABBCDBCCD已知面请问哪些平面是互相垂直的,为什么?BCDABC面面ACDABC面面BCDABD面面BCDAB面ABCCD面BCDAB面ABCD探究2：3.两个平面垂直应用举例例1:AB是⊙O的直径，PA垂直于⊙O所在的平面，点C是⊙O上不同于A,B的任一点，求证：平面PAC⊥平面PBC．PABCO4.在解题时注意应用.3.证明面面垂直要从寻找面的垂线入手;2.理解面面垂直的判定都要依赖面面垂直的定义;1.定义面面垂直是在建立在二面角的平面角的基础上的;小结：直线与平面垂直的性质平面与平面垂直的性质2.线面垂直判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么该直线与此平面垂直。1.线面垂直定义：如果一条直线和一个平面内的任何一条直线都垂直，那么称这条直线和这个平面垂直。复习回顾：3.平面与平面垂直的定义:如果两个平面所成的二面角是直角（即成直二面角），就说这两个平面互相垂直．4.两个平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直．直线与平面垂直的性质在平面内，如果两条直线同时垂直于另一条直线，那么这两条直线平行。在空间中有相同或者类似的结论吗？观察下面的长方体，找出所有标记的线面之间的位置关系。线面垂直的性质定理1：垂直于同一个平面的两条直线平行。aa//ab//ab线面垂直的性质定理2：垂直于同一条直线的两个平面平行。如果两个平面垂直，那么一个平面内的直线是否一定垂直于另一个平面?思考1：思考2：黑板所在平面与地面所在平面垂直，你能否在黑板上画一条直线与地面垂直?思考3：如果两个平面互相垂直，那么在第一个平面内垂直于交线的直线，是否垂直于第二个平面呢？[分析]在β内作BECD⊥。要证AB⊥β，只需证AB垂直于β内的两条相交直线就行。思考2：如图2，α⊥β，ABα，ABCD⊥，α∩β=CD，求证：AB⊥β。两个平面垂直的性质定理1两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．而我们已经有ABCD⊥，只需寻求另一条就够了。而我们还有αβ⊥这个条件没使用，由αβ⊥定义，则∠ABE为直角，即有ABBE⊥，也就有ABβ⊥，问题也就得到解决．思考3：设平面α⊥平面β，点P在平面α内，过点P作平面β的垂线a，直线a与平面α具有什么位置关系？βcP已知：⊥β，P∈，Pa,aβ.∈⊥求证：a∩证明：设∩β=c，过点P在平面内,作直线b⊥c，根据上面的定理有bβ.⊥因为经过一点只能有一条直线与平面β垂直，所以直线a应与直线b重合.所以a.∩abβcPba两个平面垂直的性质定理2如果两个平面互相垂直，那么经过第一个平面内一点且垂直于第二个平面的直线必在第一个平面内．两个平面垂直的性质定理1两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．1．给出下列四个命题：①垂直于同一个平面的两个平面平行；②垂直于同一条直线的两个平面平行；③垂直于同一个平面的两条直线平行；④垂直于同一条直线的两条直线平行．其中正确的命题的个数是（）．A．1B．2C．3D．4B课堂练习：2．给出下列四个命题：（其中a，b表示直线，α，β，γ表示平面）。①若ab⊥，a∥α，...