第六节带电粒子在匀强磁场中运动(习题课)VIP免费

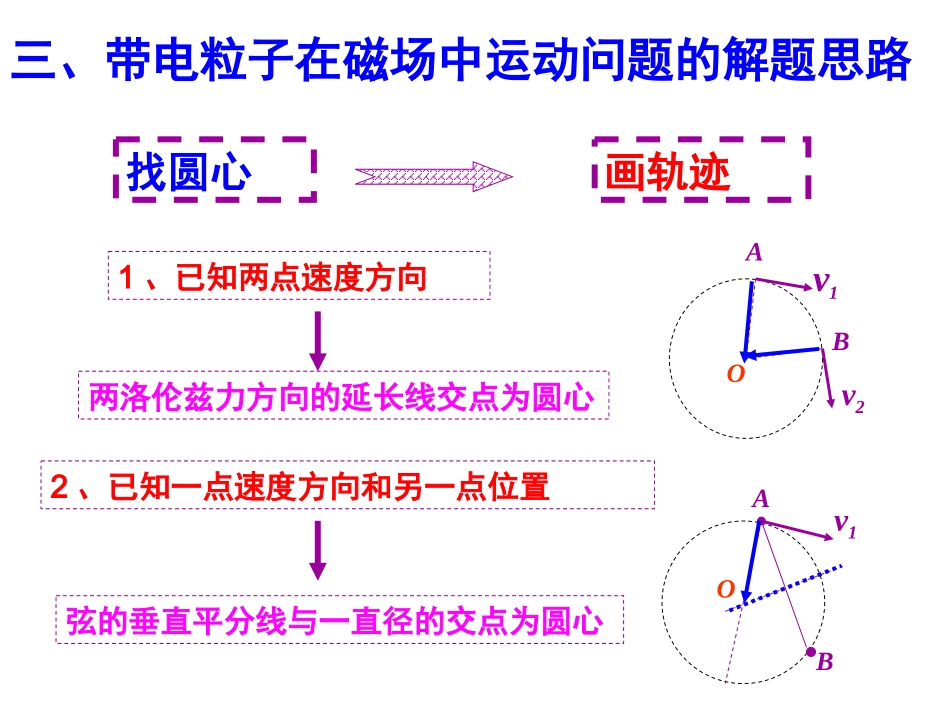
第六课时带电粒子在匀强磁场中的运动四、课堂小结：（一）、带电粒子在匀强磁场中的运动规律垂直入射磁场的带电粒子做匀速圆周运动F洛=F向2mvqvBrmvrqB22rmTvqB2tT（二）、确定带电粒子在有界磁场中运动轨迹的方法定圆心，画圆弧，求半径。三、带电粒子在磁场中运动问题的解题思路找圆心画轨迹1、已知两点速度方向2、已知一点速度方向和另一点位置两洛伦兹力方向的延长线交点为圆心弦的垂直平分线与一直径的交点为圆心v1Ov2ABv1ABO•1、找圆心：方法•2、定半径：•3、确定运动时间：Tt2qBmT2注意：θ用弧度表示几何法求半径向心力公式求半径利用v⊥R利用弦的中垂线t=（θo/360o）T（四）、确定带电粒子在有界磁场中运动轨迹的方法五．注意圆周运动中有关对称规律(1)从直线边界射入匀强磁场的粒子，从同一边界射出时，速度与边界的夹角相等，如图6－2所示．图6-2例4．一个负离子，质量为m，电量大小为q，以速率v垂直于屏S经过小孔O射入存在着匀强磁场的真空室中，如图所示。磁感应强度B的方向与离子的运动方向垂直，并垂直于图中纸面向里。（1）求离子进入磁场后到达屏S上时的位置与O点的距离。（2）如果离子进入磁场后经过时间t到达位置P，证明：直线OP与离子入射方向之间的夹角θ跟t的关系是θ=qBt/2mvPθS2θ•vOPBθSO′C画轨迹——连接OP，作垂直平分线交OS于O′半圆R=mv/qB∴OS=2R=2mv/qB∠OO′P=2θT=2πm/qBt=2θT/2π=2mθ/qB∴θ=qBt/2m解:（1）找圆心O′——定半径R——2θ例4．一个负离子，质量为m，电量大小为q，以速率v垂直于屏S经过小孔O射入存在着匀强磁场的真空室中，如图所示。磁感应强度B的方向与离子的运动方向垂直，并垂直于图中纸面向里。（1）求离子进入磁场后到达屏S上时的位置与O点的距离。（2）如果离子进入磁场后经过时间t到达位置P，证明：直线OP与离子入射方向之间的夹角θ跟t的关系是θ=qBt/2mqvB=mv2/Rt/T=2θ/2π•(2)如何求tOP？t/T=θ/2πf反馈练习2、长为L的水平极板间，有垂直纸面向内的匀强磁场，如图所示，磁场强度为B，板间距离也为L，板不带电，现有质量为m，电量为q的带负电粒子（不计重力），从左边极板间中点处垂直磁场以速度v平行极板射入磁场，欲使粒子不打在极板上，则粒子入射速度v应满足什么条件？如果欲使粒子直线飞出，怎么办呢？BvqmLLvBvqmLLvOr12rr1v=qBr/mv5qBL/4m反馈练习2、长为L的水平极板间，有垂直纸面向内的匀强磁场，如图所示，磁场强度为B，板间距离也为L，板不带电，现有质量为m，电量为q的带负电粒子（不计重力），从左边极板间中点处垂直磁场以速度v平行极板射入磁场，欲使粒子不打在极板上，则粒子入射速度v应满足什么条件？如果欲使粒子直线飞出，怎么办呢？veBmvr反馈练习3．如图所示，M、N两板相距为d，板长为5d，两板不带电，板间有垂直纸面的匀强磁场，一大群电子沿平行于板的方向从各处位置以速率v0射入板间，为了使电子都不从板间穿出，磁感应强度B的大小范围如何？（设电子质量为m，电量为e，且N板接地）反馈练习3．如图所示，M、N两板相距为d，板长为5d，两板不带电，板间有垂直纸面的匀强磁场，一大群电子沿平行于板的方向从各处位置以速率v0射入板间，为了使电子都不从板间穿出，磁感应强度B的大小范围如何？（设电子质量为m，电量为e，且N板接地）2r>dr>d/2mv0/qB>d/2B<2mv0q/dr1rqmv0/13d