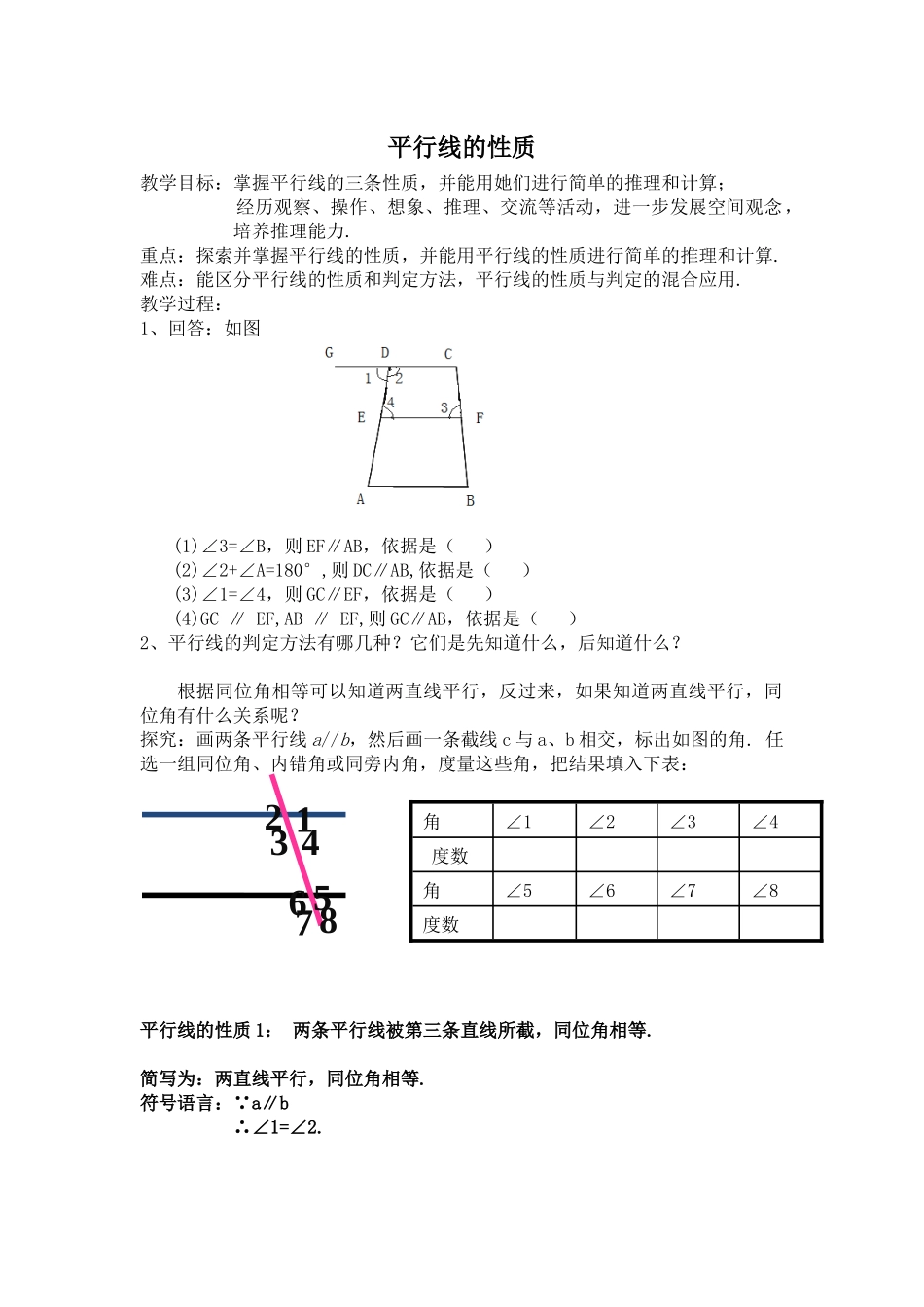
平行线的性质教学目标:掌握平行线的三条性质,并能用她们进行简单的推理和计算;经历观察、操作、想象、推理、交流等活动,进一步发展空间观念,培养推理能力.重点:探索并掌握平行线的性质,并能用平行线的性质进行简单的推理和计算.难点:能区分平行线的性质和判定方法,平行线的性质与判定的混合应用.教学过程:1、回答:如图(1)∠3=∠B,则EF∥AB,依据是()(2)∠2+∠A=180°,则DC∥AB,依据是()(3)∠1=∠4,则GC∥EF,依据是()(4)GC∥EF,AB∥EF,则GC∥AB,依据是()2、平行线的判定方法有哪几种?它们是先知道什么,后知道什么?根据同位角相等可以知道两直线平行,反过来,如果知道两直线平行,同位角有什么关系呢?探究:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角.任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:平行线的性质1:两条平行线被第三条直线所截,同位角相等.简写为:两直线平行,同位角相等.符号语言:∵a∥b∴∠1=∠2.13248576角∠1∠2∠3∠4度数角∠5∠6∠7∠8度数如图:已知a//b,那么Ð2与Ð3相等吗?为什么?平行线的性质2:两条平行线被第三条直线所截,内错角相等.b12ac3解∵ab(∥已知),∴∠1=2(∠两直线平行,同位角相等).又∵∠1=3(∠对顶角相等),∴∠2=3(∠等量代换).简写为:两直线平行,内错角相等。符号语言:∵a∥b∴∠2=∠3.如图,已知a//b,那么Ð2与Ð4有什么关系呢?为什么?解:∵a∥b(已知)∴∠1=∠2.(两直线平行,同位角相等)∵∠1+∠4=180(邻补角定义)∴∠2+∠4=180(等量代换)平行线的性质3:两条平行线被第三条直线所截,同旁内角互补.简写成:两直线平行,同旁内角互补.符号语言:∵a∥b∴∠2+∠4=180先知道后知道平行线的性质:两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.练习:b12ac4练习2.如图1,AB∥CD,∠1=45°且∠D=∠C,求出∠D,∠C,∠B的度数.1.如图,已知AB//CD,AD//BC.填空:(1)∵AB//CD(已知),∴∠1=∠___();(2)∵AD//BC(已知)∴∠2=∠___().ADCB12课堂小结:一、平行线的性质:两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.二、平行线的性质与判定的区别:已知角之间的关系(相等或互补),得到两直线平行的结论,是平行线的判定.已知两直线平行,得到角之间的关系(相等或互补)的结论,是平行线的性质.解:∵ABCD,1=45°(∥∠已知)∴∠D=45°(两直线平行,同位角相等)∵∠C=D(∠已知)∴∠C=45°(等量代换)∴∠B=180°-C=180°-45°=∠135°(两直线平行,同旁内角互补)