四川省绵阳市 高二数学下学期期末教学质量测试试卷 文试卷VIP免费

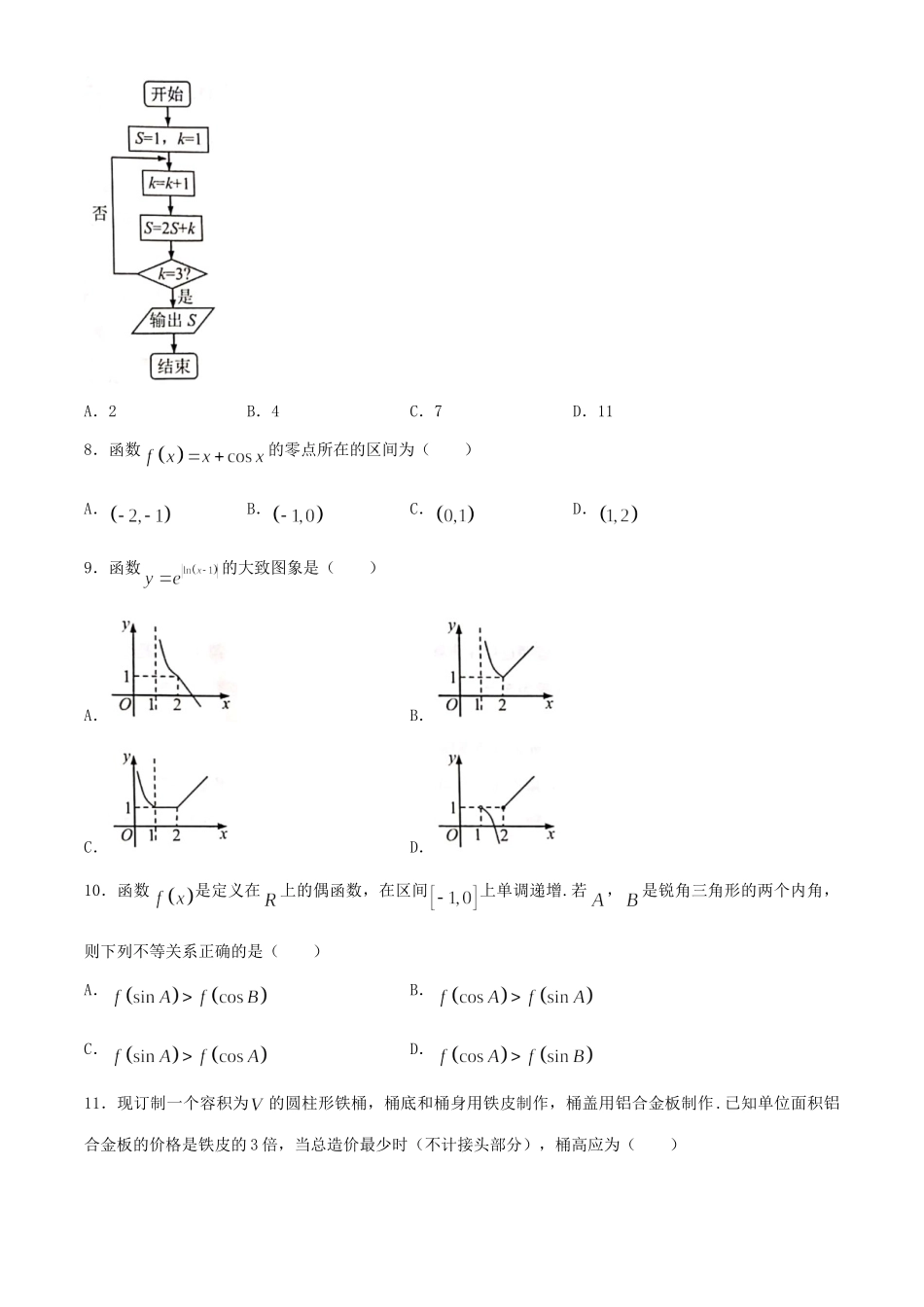
四川省绵阳市2019-2020学年高二数学下学期期末教学质量测试试题文一、选择题1．已知集合，，那么（）A．B．C．D．2．设命题：，，则为（）A．，B．，C．，D．，3．若，，则“”的一个充要条件是（）A．B．C．D．4．设函数则（）A．2B．4C．6D．185．已知函数，则（）A．－7B．－3C．－1D．46．类比推理是一种重要的推理方法.已知，，是三条互不重合的直线，则下列在平面中成立的结论类比到空间中仍然成立的是（）①若，，则；②若，，则；③若与相交，则必与其中一条相交.A．①B．①②C．①③D．②③7．执行如图所示的程序框图，输出的值为（）A．2B．4C．7D．118．函数的零点所在的区间为（）A．B．C．D．9．函数的大致图象是（）A．B．C．D．10．函数是定义在上的偶函数，在区间上单调递增.若，是锐角三角形的两个内角，则下列不等关系正确的是（）A．B．C．D．11．现订制一个容积为的圆柱形铁桶，桶底和桶身用铁皮制作，桶盖用铝合金板制作.已知单位面积铝合金板的价格是铁皮的3倍，当总造价最少时（不计接头部分），桶高应为（）A．B．C．D．12．偶函数的定义域为，周期为4，导函数为.若，且，则不等式的解集为（）A．B．C．D．二、填空题13．若复数，则______.14．已知函数，则函数的定义域为______.15．某数学小组进行社会实践调查，了解到某桶装水经营部在为如何定价发愁.进一步调研，了解到如下信息：该经营部每天的房租、人员工资等固定成本为200元，每桶水的进价是5元，销售单价与日均销售量的关系如下表：销售单价/元6789101112日均销售量/桶480440400360320280240根据以上信息，你认为该经营部把桶装水定价为______元/桶时能获得最大利润.16．已知函数，若，都有成立，则的取值范围是______.三、解答题17．小王进行投资研究，发现投资开餐馆的收益与投资金额的关系是，的部分图象如图1；投资运输运营的收益与投资金额的关系是，的部分图象如图2.（收益与投资金额单位：万元）（1）求，的解析式；（2）小王准备将自己的存款100万元全部投资餐馆和运输运营，如何分配才能使投资获得最大收益，其最大收益为多少万元？18．已知函数在处有极值，且曲线在点处的切线与直线平行.（1）求；（2）求函数在区间上的最值.19．已知函数，其中，为自然对数的底数.（1）试讨论的单调性；（2）是否存在正整数，使得对一切恒成立？若存在，求出的最大值；若不存在，请说明理由.20．在平面直角坐标系中，以原点为极点，轴的正半轴为极轴，建立极坐标系.已知曲线的极坐标方程为.（1）求曲线的直角坐标方程；（2）若直线的参数方程为（为参数），设直线与曲线的交点为，，求.21．已知函数.（1）若，解关于的不等式；（2）证明：对任意，.绵阳市高中2018级第二学年末教学质量测试文科数学参考答案一、选择题1~5ACACB6~10ADBBD11~12CA二、填空题13．14．15．11.516．三、解答题17．（1）由图1，得，解得，∴，由图2，得，解得，∴.（2）设最大收益为万元，投资餐馆资金为万元，投资运输运营万元.由题意得.∴，由，解得，由，解得，∴当时，.∴投资餐馆资金为93.75万元，投资运输运营6.25万元，才能使投资获得最大收益，其最大收益为156.25万元.18．解：（1）函数的导函数为，由题意得即解得∴.（2）由（1）得.当时，由，得或；由，得.∴函数在处取得极大值，在处取极小值，∴，，，，∴函数在区间上的最小值为－2，最大值为1.19．解：（1）.①当时，恒成立，在上单调递增；②当时，令，则，当时，，单调递减；当时，，单调递.综上，当时，在上单调递增；当时，在上单调递减，在上单调递增.（2）要使在上恒成立，即使在上恒成立，令，则.①当时，，由知在单减，在单增.∴，∴时满足题意.②当时，考查时，函数的取值情况：∵，∴，.又，∴，即，∴当时，在上单调递增.取，则函数在上单增，∵，且，∴不能恒成立.综上，的最大正整数值为2.20．解：（1）∵曲线的极坐标方程为，∴，∵，，∴，即.（2）将直线的参数方程曲线的直角坐标方程，即，整理得，解得或.∴.21．解：（1）当时，.当时，，解得，综合得；当时，，解得，综合得；当时，，解得，综合得；∴综上所述，不等式的解集为.（2）∵，∴，∵，∴，∴对任意，.