山东省新泰二中高一数学上学期期中试卷VIP免费

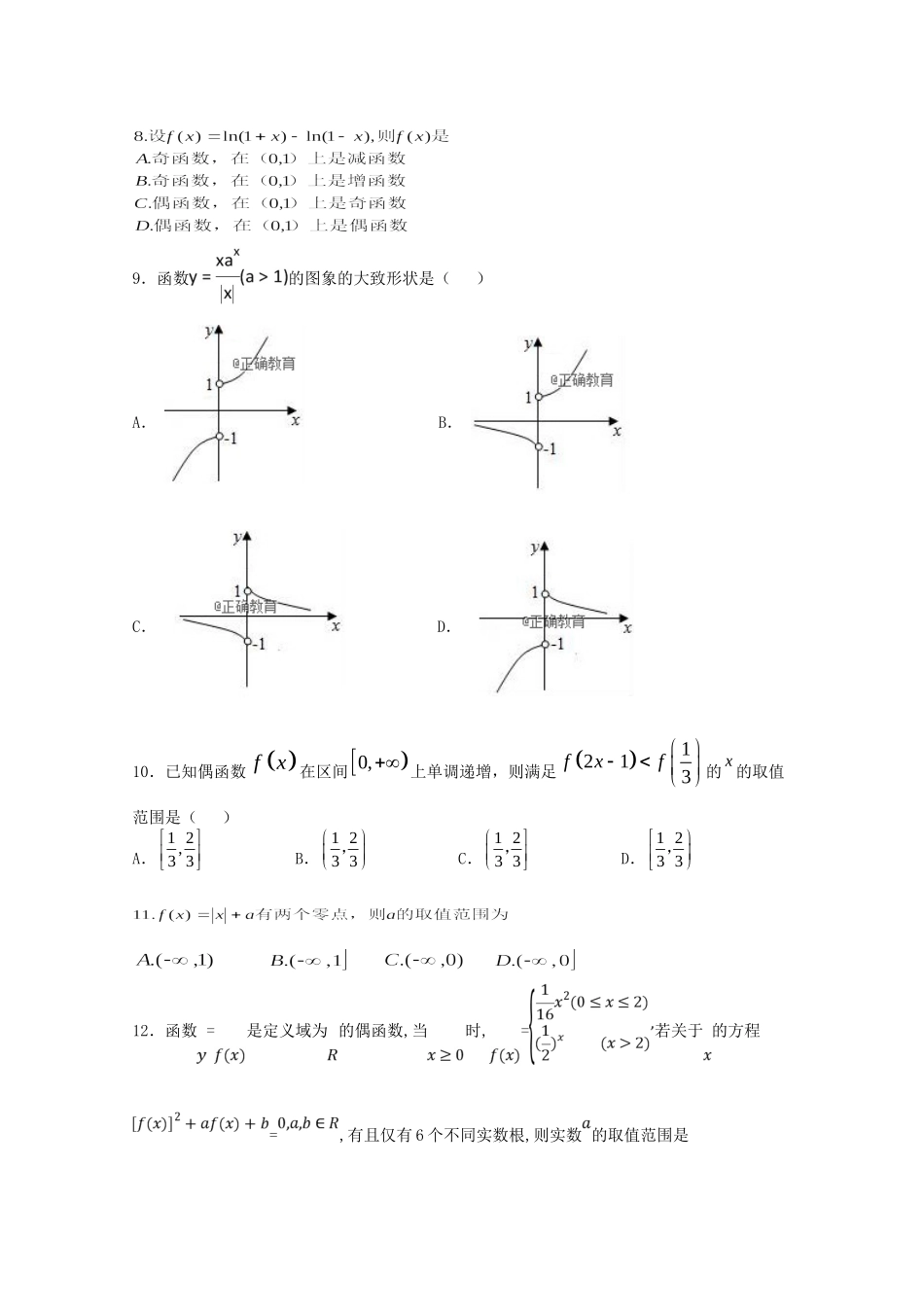
山东省新泰二中2018-2019学年高一数学上学期期中试题一．选择题（每小题5分，共60分）1．集合,，则（）A.B.C.D.2．下列各组函数中，相等的是（）A．B．C．D．3．已知函数为奇函数，当时，，则（）A．2B．1C．0D．-24．函数的定义域为（）A.B.C.D.5．已知，，,则的大小关系是（）A.B.C.D.6．函数的零点所在的区间为（）.A.B.C.D.7.函数的单调减区间为()ABCD9．函数的图象的大致形状是（）A．B．C．D．10．已知偶函数fx在区间0,上单调递增，则满足1213fxf的x的取值范围是（）A．12,33B．1233，C．1233，D．1233，12．函数=是定义域为的偶函数,当时,=若关于的方程=,有且仅有6个不同实数根,则实数的取值范围是A.B.C.D二、填空题（每题5分，共4题20分）13.若幂函数的图象经过点，则的值为__________．14.其图像过定点__________．15．设函数)2(1)21()2()2()(xxxaxfx是R上的单调递减函数，则实数a的取值范围为__________．16．设，且，则=__________．三、解答题（本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤）17．（本题满分10分）计算题:(1)(2)已知,用表示．18.（本题满分12分）已知集合，集合.（1）求当时，;（2）若,求实数的取值范围.19.（本题满分12分）已知定义域为的奇函数，当时,.（1）当0x时，求函数)(xf的解析式；（2）解方程．20.（本题满分12分）设函数(1)求t的取值范围；(2)求f(x)的值域．21.（本题满分12分）已知函数，是奇函数．（1）求的值；（2）证明：是区间上的减函数；（3）若，求实数的取值范围．22.（本题满分12分）某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t，P)，点(t，P)落在下图中的两条线段上；该股票在30天内的日交易量Q(万股)与时间t(天)的部分数据如下表所示：(1)根据提供的图象，写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式；(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式；(3)在(2)的结论下，用y表示该股票日交易额(万元)，写出y关于t的函数关系式，并求在这30天中第几天日交易额最大，最大值是多少？参考答案1-5ACDCA6-10DCBBB11-12CA13、14、（-2，-1）15、(-∞，813]16、10017.(1)(2)∵==,∴===.18.解：(1)当时，，...........................2分∴.....................................................................4分；......................................................................6分(2)由可得,.................................................8分则，.......................................................................10分解得，即............................................................11分∴实数m的取值范围为.................................................12分19.解：(1)当时，，函数是定义在R上的奇函数，∵当时,，∴....................6分(2)当时,，解得，满足题意;....................................9分时，，解得，........................11分所以方程的解为0,5或-5.............12分20.解：(1)因为t＝log2x，≤x≤4，所以log2≤t≤log24，即－2≤t≤2.——————4分(2)函数f(x)＝log2(4x)·log2(2x)＝(log24＋log2x)(log22＋log2x)＝(log2x＋2)(log2x＋1)＝(log2x)2＋3log2x＋2.又t＝log2x，则y＝t2＋3t＋2＝－(－2≤t≤2)．当t＝－，即log2x＝－，x＝2－时，f(x)min＝－；当t＝2，即log2x＝2，x＝4时，f(x)min＝12.综上可得，函数f(x)的值域为.————————12分21.解：(1)∵函数，是奇函数，∴，且，即.......................................................4分(2)证明：设任意的，且，则，.................................6分∴.∴是区间上的减函数...........................................8分(3)构造函数，则是奇函数且在定义域内单调递减，原不等式等价于，....................................9分∴，即有，∴，......................11分则实数m的取值范围是..............................................12分22.解：（1）------------------------------------4分（2）设Q=at+b（a，b为常数），将（4，36）与（10，30）的坐标代入，得．日交易量Q（万股）与时间t（天）的一次函数关系式为Q=40﹣t，0＜t≤30，t∈N*．---7分（3）由（1）（2）可得即---------------------------------9分当0＜t≤20时，当t=15时，ymax=125；当上是减函数，y（20）=120＜y（15）=125．-------------------------------------------------------------------11分所以，第15日交易额最大，最大值为125万元．------------------------------12