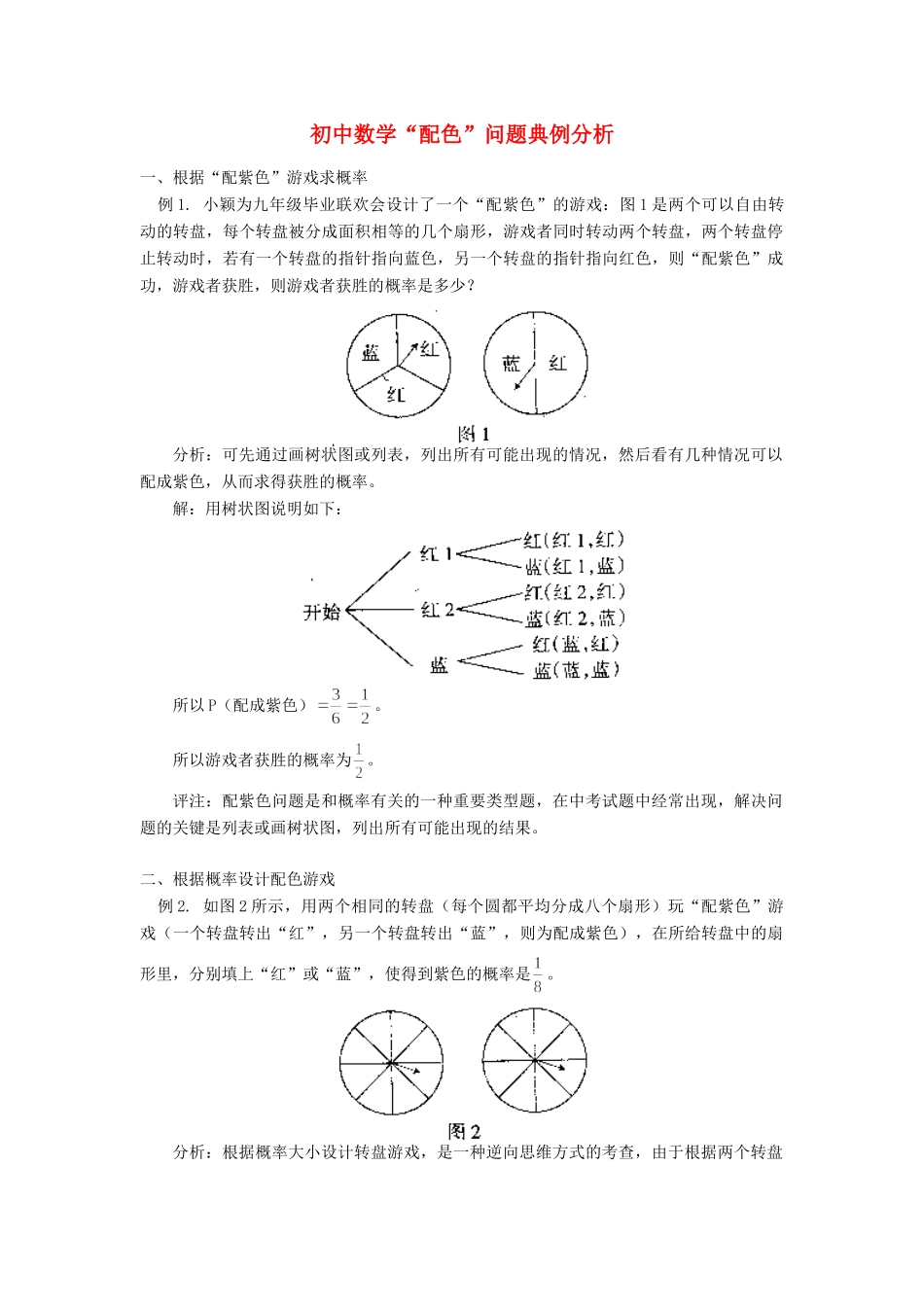
初中数学“配色”问题典例分析一、根据“配紫色”游戏求概率例1.小颖为九年级毕业联欢会设计了一个“配紫色”的游戏:图1是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,游戏者同时转动两个转盘,两个转盘停止转动时,若有一个转盘的指针指向蓝色,另一个转盘的指针指向红色,则“配紫色”成功,游戏者获胜,则游戏者获胜的概率是多少?分析:可先通过画树状图或列表,列出所有可能出现的情况,然后看有几种情况可以配成紫色,从而求得获胜的概率。解:用树状图说明如下:所以P(配成紫色)。所以游戏者获胜的概率为。评注:配紫色问题是和概率有关的一种重要类型题,在中考试题中经常出现,解决问题的关键是列表或画树状图,列出所有可能出现的结果。二、根据概率设计配色游戏例2.如图2所示,用两个相同的转盘(每个圆都平均分成八个扇形)玩“配紫色”游戏(一个转盘转出“红”,另一个转盘转出“蓝”,则为配成紫色),在所给转盘中的扇形里,分别填上“红”或“蓝”,使得到紫色的概率是。分析:根据概率大小设计转盘游戏,是一种逆向思维方式的考查,由于根据两个转盘设计出配成紫色的概率是,而,所以有多种不同的设计方案。解:(方案1)如图3,一个转盘的八个扇形都填“红”,另一个转盘的一个扇形填“蓝”,余下的七个扇形不填或填其他颜色。(方案2)一个转盘的八个扇形都填“蓝”,另一个转盘的一个扇形填“红”,余下的七个扇形不填或填其他颜色。(方案3)一个转盘的两个扇形填“蓝”,另一个转盘填四个“红”,其余的扇形不填或填其他颜色。评注:根据概率大小设计“配紫色”游戏,设计的方法比较多,只要设计出一种符合要求的即可。