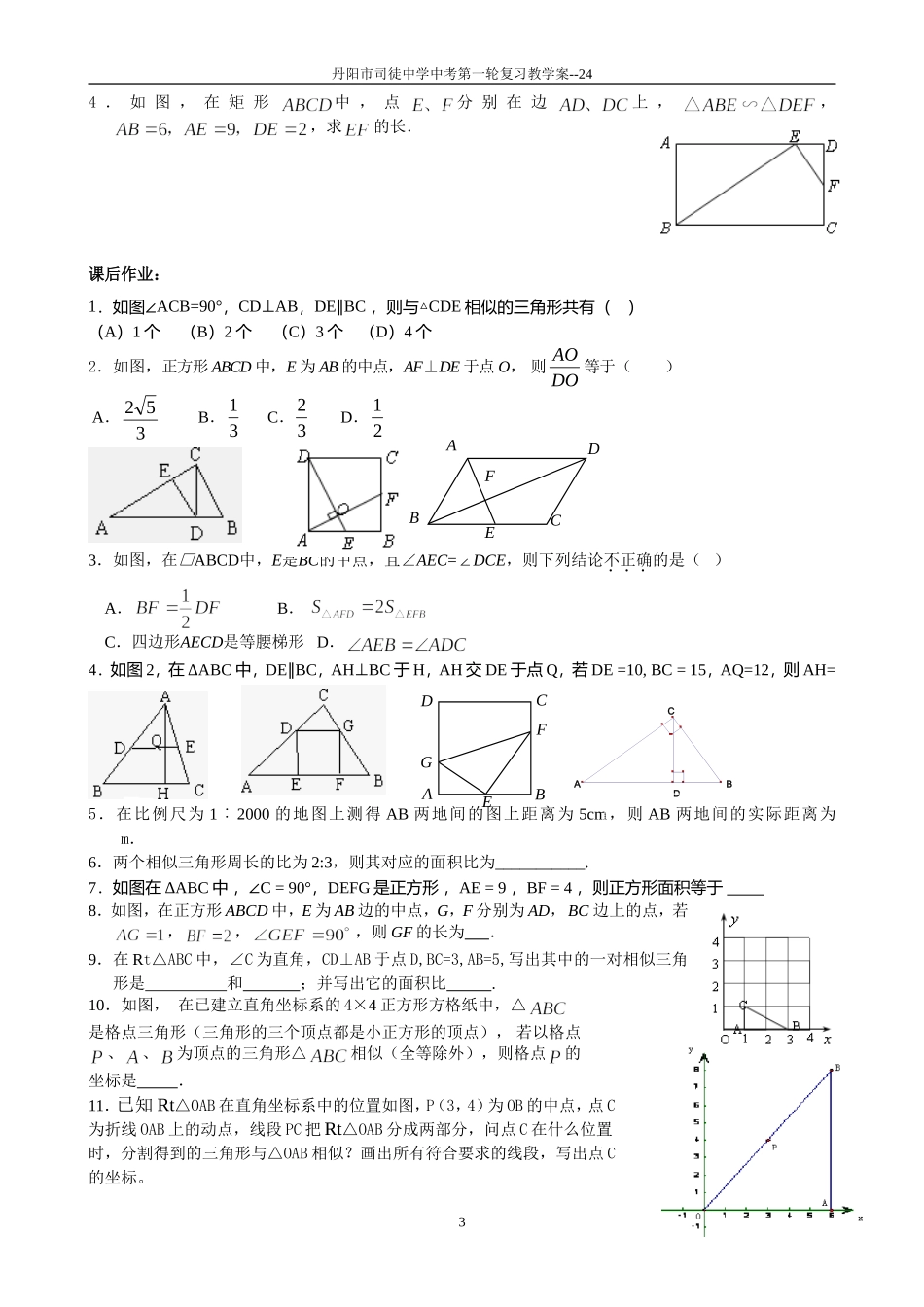
FEBACD丹阳市司徒中学中考第一轮复习教学案--24课时24相似三角形【基础知识】一、相似三角形的定义三边对应成_________,三个角对应________的两个三角形叫做相似三角形.二、相似三角形的判定方法1.两个角对应相等的两个三角形__________.2.两边对应成_________且夹角相等的两个三角形相似.3.三边对应成比例的两个三角形___________.三、相似三角形的性质1.相似三角形的对应边_________,对应角________.2.相似三角形的对应边的比叫做________,一般用k表示.3.相似三角形的对应角平分线,对应边的________线,对应边上的_______线的比等于_______比,周长之比也等于________比,面积比等于_________.4.若DE∥BC(A型和X型)则______________.四、位似图形1、定义:两个多边形不仅相似,而且对应顶点间连线相交于,对应边互相(或在一条直线上),像这样的两个图形叫做位似图形,这个点叫做。2、位似与相似的关系:位似是一种的相似,构成位似的两个图形不仅相似,而且对应点的连线相交于一点,对应边互相(或在一条上)3、位似图形的性质:(1)位似图形上的任意一对对应点到位似中心的距离的比等于____________;(2)位似图形对应点的连线或延长线相交于一点;(3)位似图形对应边________(或在一条直线上);(4)位似图形对应角【知识应用】1.若x是a、b、c的第四项比例项,且a=b,b=3,c=5,则x=2.若2a=3b=4c(a≠0)则=___________3.在△ABC中,AB=8,AC=6,点D在AC上且AD=2,如果要在AB上找一点E,使△ADE∽ΔABC,那么AE等于()(A)83(B)32(C)83或32(D)38或234.在△ABC与△A′B′C′中,有下列条件:(1);(2);(3)∠A=∠A′;(4)∠C=∠C′.如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有多少组()A.1B.2C.3D.45.矩形ABCD中,E是BC边上一点,AE⊥DE,若BE∶EC=4∶1,则AB∶BC=6.如图,□ABCD中,E为AD的中点.已知△DEF的面积为S,则△DCF的面积为()A.SB.2SC.3SD.4S.7.如图,在DABC中,已知DE∥BC,AD=4,DB=8,DE=3,1EDCBADCBAEADCBEADCB丹阳市司徒中学中考第一轮复习教学案--24(1)求ADAB的值,(2)求BC的长【例题讲解】例1.在△ABC和△DEF中,已知∠A=∠D,AB=4,AC=3,DE=1,当DF等于多少时,这两个三角形相似.例2.在13×13的网格中,已知△ABC和点M(1,2).(1)以点M为位似中心,位似比为2,画出△ABC的位似图形△A′B′C′;(2)写出△A′B′C′的各顶点坐标.例3.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?【质疑反馈】:1.如图小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m、与旗杆相距22m,则旗杆的高为()A.12mB.10mC.8mD.7m2.如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是()A.2cm2B.4cm2C.8cm2D.16cm23.如图,Rt△ABAC中,AB⊥AC,AB=3,AC=4,P是BC边上一点,作PE⊥AB于E,PD⊥AC于D,设BP=x,则PD+PE=()A.B.C.D.2ABCDEP丹阳市司徒中学中考第一轮复习教学案--244.如图,在矩形中,点分别在边上,,,求的长.课后作业:1.如图∠ACB=90°,CD⊥AB,DE∥BC,则与△CDE相似的三角形共有()(A)1个(B)2个(C)3个(D)4个2.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则DOAO等于()A.352B.31C.32D.213.如图,在□ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是()A.B.C.四边形AECD是等腰梯形D.4.如图2,在ΔABC中,DE∥BC,AH⊥BC于H,AH交DE于点Q,若DE=10,BC=15,AQ=12,则AH=5.在比例尺为1︰2000的地图上测得AB两地间的图上距离为5cm,则AB两地间的实际距离为m.6.两个相似三角形周长的比为2:3,则其对应的面积比为___________.7.如图在ΔABC中,∠C=90°,DEFG是正方形,AE=9,BF=4,则正方形面积等于8.如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点...