立体图形展开---勾股定理应用(4)VIP免费

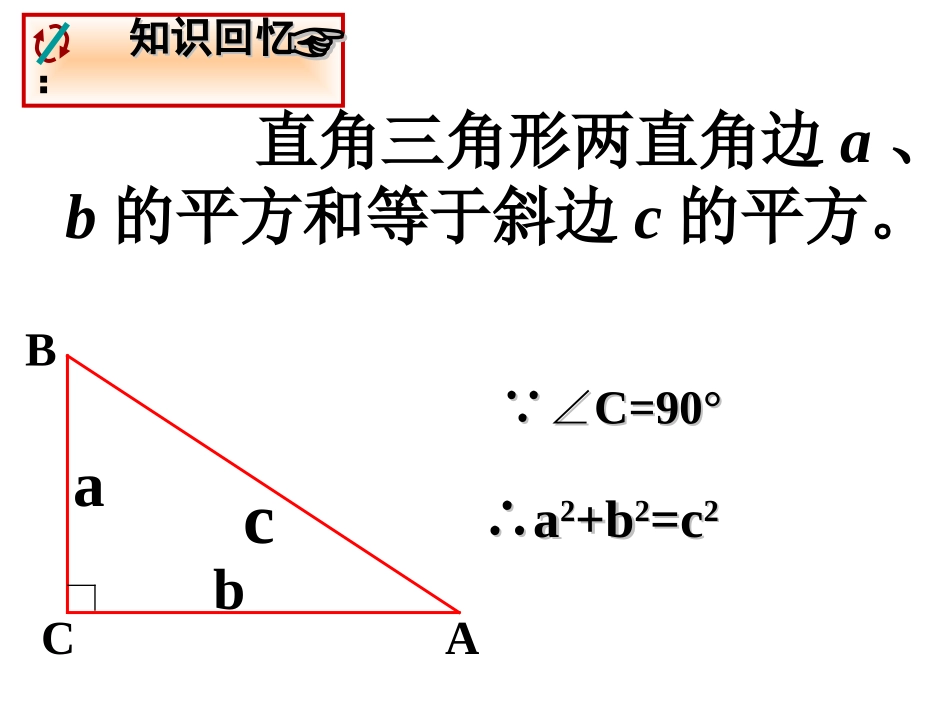
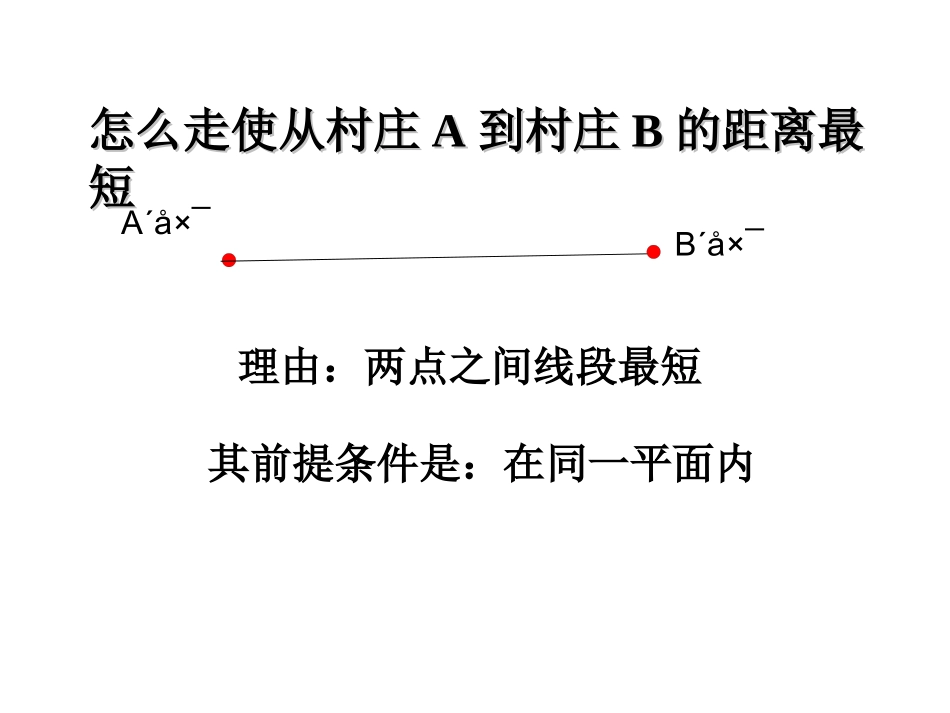
勾股定理应用（4）知识回忆知识回忆：☞☞cab直角三角形两直角边a、b的平方和等于斜边c的平方。CAB∵∠∵∠C=90°C=90°∴∴aa22+b+b22=c=c22A´åׯB´åׯ怎么走使从村庄怎么走使从村庄AA到村庄到村庄BB的距离最的距离最短短理由：两点之间线段最短其前提条件是：在同一平面内如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(取3）是()A.20cmB.10cmC.14cmD.无法确定BB8OA2蛋糕ACB８周长的一半６圆柱(锥)中的最值问题例4、如图，一只蚂蚁从实心长方体的顶点A出发，沿长方体的表面爬到对角顶点C1处（三条棱长如图所示），问怎样走路线最短？最短路线长为多少？ABA1B1DCD1C1214长方体中的最值问题能否直间从A走到C1？B1D1AC1BA1B1C1AA1CBCC1ADB1B图1图2图3按图1来计算2214(21)255AC221(42)137AC按图2来计算按图3来计算221(41)229AC如果长方形的长、宽、高分别是a、b、c（a＞b＞c），你能求出蚂蚁从顶点A到C1的最短路径吗？从A到C1的最短路径是：22)cb(a注意：b和c是a、b、c中较短的两条边。如图是一个三级台阶，它的每一级的长宽和高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是多少？2032AB２０２32323ＡＢＣ∵AB2=AC2+BC2=625,∴AB=25.台阶中的最值问题立体图形两点距离平面图形两点之间的距离转化展开图展开思想：1.几何体的表面路径最短的问题，一般展开表面成平面。2.利用两点之间线段最短，及勾股定理求解。如图，长方体的长为15cm，宽为10cm，高为20cm，点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是多少？1020BAC155长方体中的最值问题BAC1551020B5B51020ACEFE1020ACFAECB2015105②BA2010155AB=√202+152=√625AB=√102+252=√7251020BAC155①A2010155B③AB=√302+52=√92515③BA20105