幂的乘方-(2)VIP免费

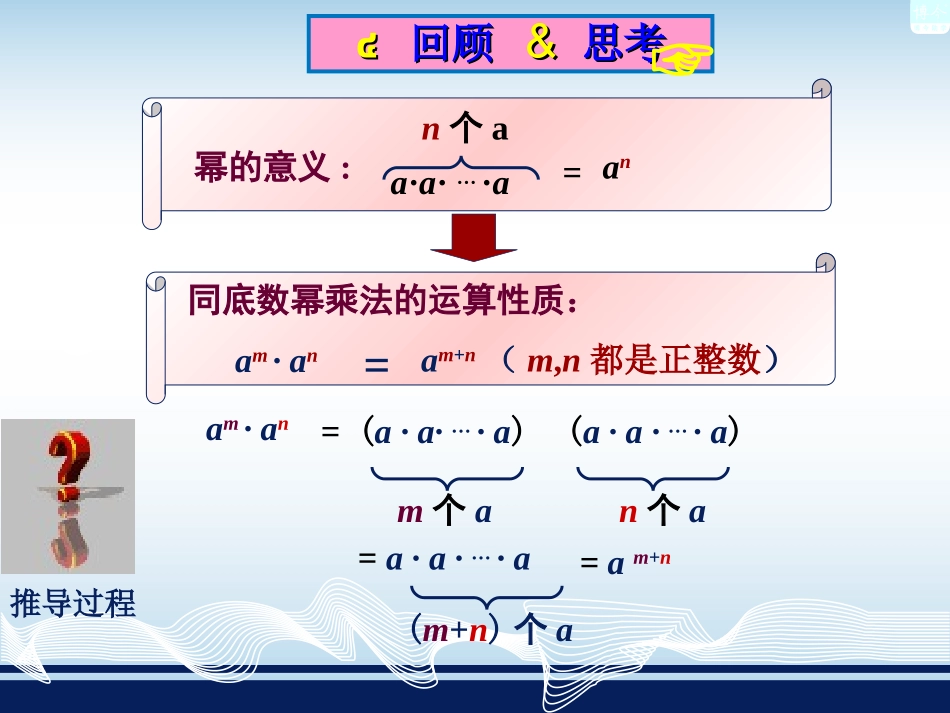
本节内容2.1.2人教版数学七年级（下）主讲：枣阳市太平镇中学ghqam·an(a·a·…·a)n个a=(a·a·…·a)m个a=a·a·…·a(m+n)个a=am+n幂的意义:a·a·…·an个aan=同底数幂乘法的运算性质：am·an=am+n（m,n都是正整数）推导过程๔๔回顾回顾&&思考思考☞2am合并同类项法则a8同底数幂乘法的法则填空：1.am+am=_____,依据________________.2.a3·a5=____,依据_______________做一做动脑筋计算下列各式，并说明理由.（1）(62)4;（2）(a2)3;（3）(am)2;解：(1)(62)4(2)(a2)3(3)(am)2=62·62·62·62=62+2+2+2=68=a2·a2·a2=a2+2+2=a6=am·am=am+m=a2m;猜想amn探究(am)n＝幂的意义同底数幂的乘法(102)3=102×102×102=102+2+2=102×3=106(根据).(根据).同底数幂的乘法性质幂的意义2、(102)3=106，为什么？动脑筋1、(102)3代表什么意义？说一说怎样计算(a3)4？(a3)4=(a3·a3·a3·a3)(乘方的意义)4个a3=a3+3+3+3(同底数幂的乘法法则)=a3×4=a12.也就是(a3)4=a3×4.也就是(a3)4=a3×4.如何证明刚才的猜想呢?(am)n=am·am·…·am=am+m+…+m=amn(m，n都是正整数).n个amn个m探究（幂的意义）（同底数幂的乘法性质）你能归纳下这个法则吗？((am)n=amn(m、n是正整数)..结论幂的乘方，底数不变，指数相乘．幂的乘方，底数不变，指数相乘．于是，我们得到幂的乘方法则：(am)n=amn(m，n都是正整数).(am)n=amn(m，n都是正整数).幂的乘方，底数不变，指数相乘．幂的乘方，底数不变，指数相乘．即：am·an=am+n（m，n都是正整数).即：am·an=am+n（m，n都是正整数).同底数幂相乘，底数不变，指数相加.同底数幂相乘，底数不变，指数相加.同底数幂的乘法和幂的乘方的区别：即：(am)n=amn(m，n都是正整数).即：(am)n=amn(m，n都是正整数).同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点？同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点？说一说1、从底数看：底数不变（共同点）2、从指数看同底数幂的乘法，指数相加幂的乘方，指数相乘（不同点）(1)(102)3(2)(b5)5(3)(an)3=102×3=106;解：(102)3=b5×5=b25;(b5)5解：=an×3=a3n;解：(an)3举例例1计算：(4)-(x2)m(5)(y2)3·y(6)2(a2)6-(a3)4=-x2×m=-x2m;解：-(x2)m=y2×3·y=y6·y=y7;解：(y2)3·y=2a2×6-a3×4=2a12-a12=a12.解：2(a2)6–(a3)4不对不对不对不对练一练1.1.判断判断下面计算是否正确？如果不对，怎样改正？下面计算是否正确？如果不对，怎样改正？（1）((xx33))33==xx66；（2）(104)3=107；（3）aa66··aa44==aa2424；（4）(x2)3·(-x)2=-x82.填空：（1）(104)3=；（2）(a3)3=；（3）-(x3)6=；（4）(x2)3·(-x)3=.1012a9x18-x9应该是：xx99应该是：1012应该是：aa1010应该是：x8进步的阶梯（1）＝1016＝x4m＝a10＝221＝x18＝(a＋b)81.计算：⑴(104)4⑵(xm)4（m是正整数）⑶(a2)5⑷(23)7⑸(x3)6⑹[(a＋b)2]4随堂练习随堂练习【【例例22】】计算：计算：((22))((－－xx22))33==((11))((－－xx33))22==xx3×3×22==xx66((33))－－((yy22))33==－－yy22×3×3==－－yy66-xx22××33==-xx66(4)(4)––((yy33))22==–yy66=-yy33××22(a(amm))nn==aamnmn((m,nm,n都是正整数都是正整数))注意符号注意符号23))(1(x解：解：32))(2(x32)()3(y23)()4(y进步的阶梯（2）看谁对的多＝-1010＝a12＝-a10＝-218＝x181.计算：⑴(-102)5⑵(-a3)4⑶-(a2)5⑷-(23)6⑸(x3)62.下列计算是否正确，如有错误，请改正.⑴(a5)2＝a7;(a5)2＝a10⑵a5·a2＝a10；a5·a2＝a7⑶(－a2)3＝a6；(－a2)3＝－a6⑷a7＋a3＝a10；无法计算例3计算：(1)x2·x4＋(x3)2;解：x2·x4＋(x3)2=x2＋4+x3×2=x6+x6=2x6;---合并同类项幂的乘方同底数幂相乘---幂的乘方---同底数幂相乘(2)(a3)3·(a4)3=a3×3·a4×3=a9·a12=a9+12=a21.解：(a3)3·(a4)3随堂练习随堂练习3524))(1(mmm2253)())(2(aa（（33））x·xx·x44–x–x22·x·x33..计算：若(am)n=amn=anm=(am)n则amn=(an)m6245113例如:x12=(x2)()=(x6)()=(x3)()=(x4)()=x7•x()=x•x()幂的乘方的推广幂的乘方的推广[(am)n]p=(amn)p=amnp（m,n,p为正整数）432])[(a432432)(])[(aa4646)(aa24a同样：am+n=am·an（m，n都是正整数).例：((aamm))nn==aamnmn幂的乘方幂的乘方，底数不变，指数相乘．同底数幂相乘，底数不变，指数相加.即：am·an=am+n（m，n都是正整数).作业：P321、2、3、p40A2(1)、(2)