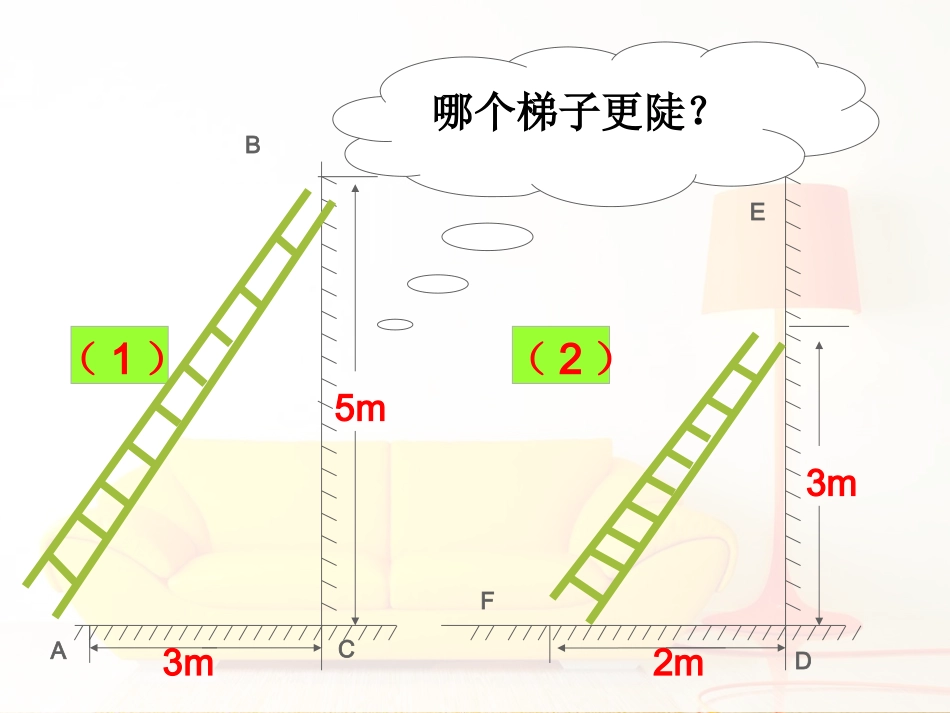
鸟儿因为翅膀而飞翔人类因为思考而飞翔风筝因为风儿而飞翔让我们一起想象,让我们一起飞翔!10m1m5m10m(1)(2)哪个梯子更陡?比眼力比速度:一一、5m3mABC3m2mEFD(1)(2)哪个梯子更陡?枞阳县陈洲初中黄峰2016.11.26AB1C1C2B2(1)Rt△AB1C1和Rt△AB2C2有什么关系?(2)和有什么关系?111ACCB222ACCB(3)如果改变点B2在梯子上的位置,这种关系还成立吗?探索与思考∙RtAB△1C1RtAB∽△2C2探索与思考111222ACCBACCB二、二、AB1C1C2B2(1)Rt△AB1C1和Rt△AB2C2有什么关系?(2)和有什么关系?111ACCB222ACCB(3)如果改变点B2在梯子上的位置,这种关系还成立吗?探索与思考∙RtAB△1C1RtAB∽△2C2探索与思考111222ACCBACCBAB1C1C2B2(1)Rt△AB1C1和Rt△AB2C2有什么关系?(2)和有什么关系?111ACCB222ACCB(3)如果改变点B2在梯子上的位置,这种关系还成立吗?探索与思考∙RtAB△1C1RtAB∽△2C2探索与思考111222ACCBACCBAB1C1C2B2(1)Rt△AB1C1和Rt△AB2C2有什么关系?(2)和有什么关系?111ACCB222ACCB(3)如果改变点B2在梯子上的位置,这种关系还成立吗?探索与思考∙RtAB△1C1RtAB∽△2C2探索与思考111222ACCBACCBAB1C1C2B2(1)Rt△AB1C1和Rt△AB2C2有什么关系?(2)和有什么关系?111ACCB222ACCB(3)如果改变点B2在梯子上的位置,这种关系还成立吗?探索与思考∙RtAB△1C1RtAB∽△2C2探索与思考111222ACCBACCB在这些直角三角形中,当锐角A的大小确定后,无论直角三角形的大小怎样变化,B2C2与AC2的比值总是一个固定值。ABC∠A的对边∠A的邻边在RtABC△中,如果锐角A确定,那么,∠A的对边与邻边的比值也随之确定,这个比叫做∠A的正切.记作:tanAab斜边c读?baACBCAAA的邻边的对边tan正切的定义三、1)tanA是一个完整的符号,它表示是一个完整的符号,它表示∠∠AA的的正切,正切,我们我们习惯省略去角的符号习惯省略去角的符号““∠”。但∠”。但∠∠BACBAC的正切应表示为的正切应表示为::tanBAC∠tanBAC∠,,1∠1∠的正的正切表示为切表示为::tan1∠tan1∠22))tanAtanA没有单位,它表示一个比值,即没有单位,它表示一个比值,即直角三角形中直角三角形中∠∠AA的对边与邻边的比。的对边与邻边的比。33))tanAtanA不能看成不能看成““tan”tan”乘以乘以““AA””,,不不能写成能写成tan•Atan•A温馨提示正切经常用来描述坡面的坡度。的比叫做坡面的和水平长度坡面的铅直高度lhtanii坡度(或坡比),记作,即(坡度通常写成的形式)坡面与水平面的夹角叫做坡角(或称倾斜角),记作α,坡度()越大,坡角α越大,坡面就。lhi:越陡5m3mABC3m2mEFD(1)(2)哪个梯子更陡?ABC在RtABC△中∠C=90°BC=3,AC=4,求tanA和tanB。34例题讲解四、四、BC1.在Rt△ABC中∠C=90°AC=5,AB=13,tanA=(),tanB=()5125A1312应用与巩固125五、五、2.在RtABC△中∠C=90°AC=12,tanA=,求BC43CBACBA变换:在RtABC△中∠C=90°AB=15,tanA=,求BC、AC43ABC6553.如图:求tanC=()33D41.如图,某人从山脚下的点A走了200m后到达山顶的点B.已知山顶B到山脚下的垂直距离是55m,求山坡的坡度.ABC┌2.在RtABC△中,C=90∠°,tanA和tanB有什么关系?为什么?ABC┌六、练习六、练习与思考与思考本节课学习了哪些内容?你有什么收获?还有哪些疑问?小结与评价