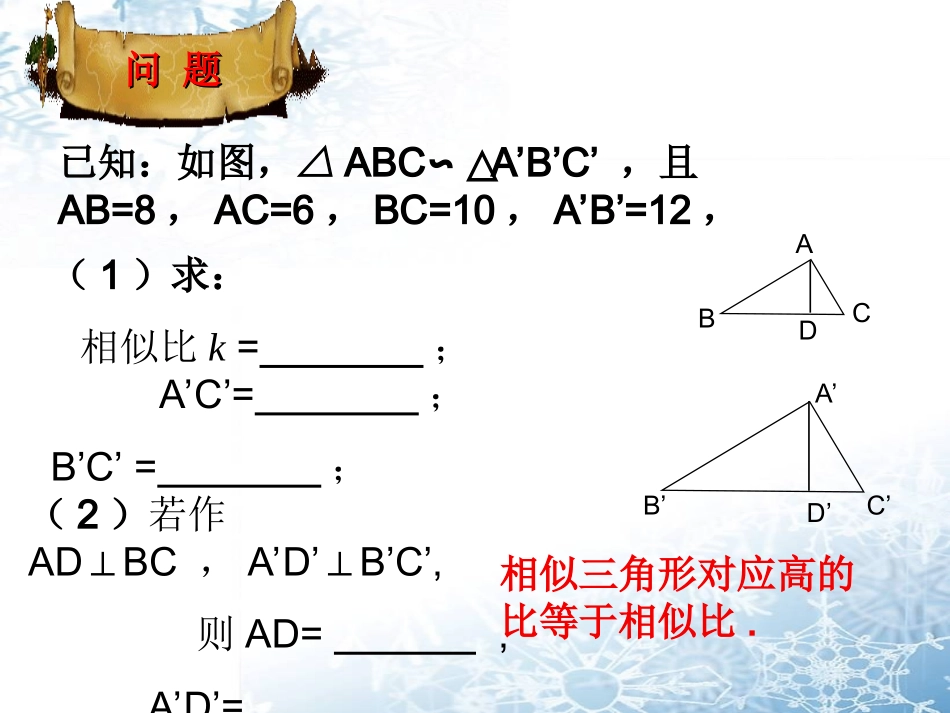
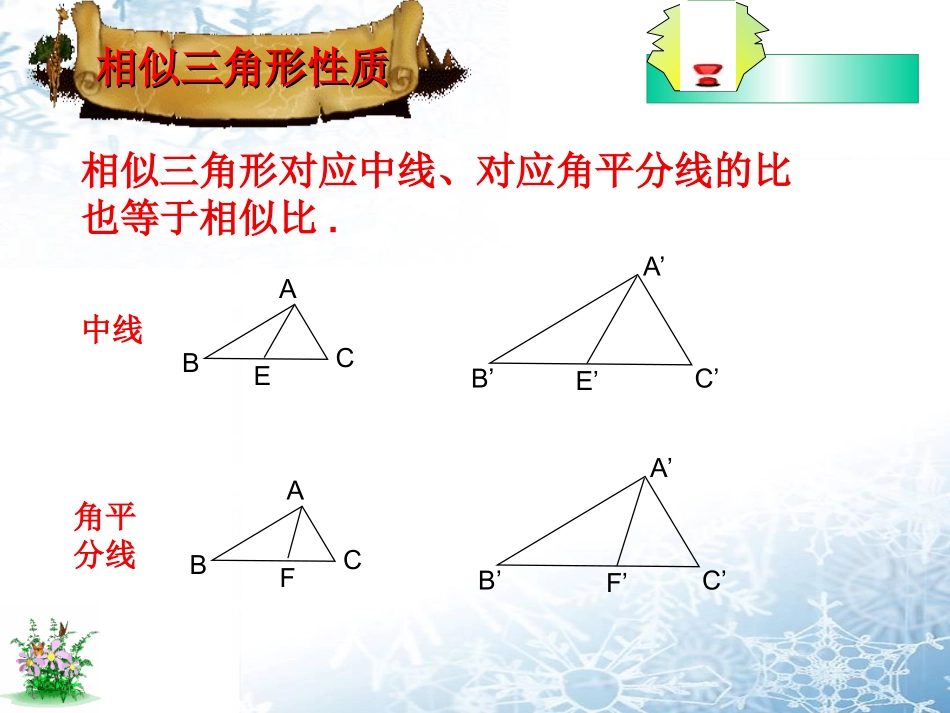
相似三角形的性质已知:如图,△ABC∽△A’B’C’,且AB=8,AC=6,BC=10,A’B’=12,问题问题(1)求:相似比k=;A’C’=;B’C’=;(2)若作ADBC⊥,A’D’B’C’,⊥则AD=,A’D’=.ABCA’B’C’D’D相似三角形对应高的比等于相似比.相似三角形性质相似三角形性质ABCEA’B’C’E’ABCFA’B’C’F’相似三角形对应中线、对应角平分线的比也等于相似比.中线角平分线相似三角形性质相似三角形性质ABCDA’B’C’D’已知:如图,△ABC∽△A’B’C’,且AB=8,AC=6,BC=10,A’B’=12,问:还成立吗?还成立吗?kCCCBAABC'''2'''kSSCBAABC结论:相似三角形的周长比等于相似比,面积比等于相似比的平方.即kSSCBAABC'''相似三角形性质相似三角形性质试一试试一试:1、一个三角形的各边长扩大为原来的5倍,则这个三角形的角平分线扩大为原来的倍,面积扩大为原来的倍.2、已知△ABCA′B′C′∽△,它们的周长分别为56cm和72cm,那么它们的面积的比.3、如果两个相似多边形的面积之比为3:4,那么它们的周长之比为.相似三角形性质相似三角形性质例:如图,在△ABC和△DEF中,AB=2DE,AC=2DF,且A=∠D,若△ABC的边BC上的高为6,面积为,求△DEF的边EF上的高和面积.512ABCDEF归纳小结归纳小结相似三角形的性质相似三角形的性质(对应线段的比、周长比、面积比)(对应线段的比、周长比、面积比)说说这一课的收获。数学方法:从特珠到一般探究问题的方法作业:见课堂反馈布置作业布置作业