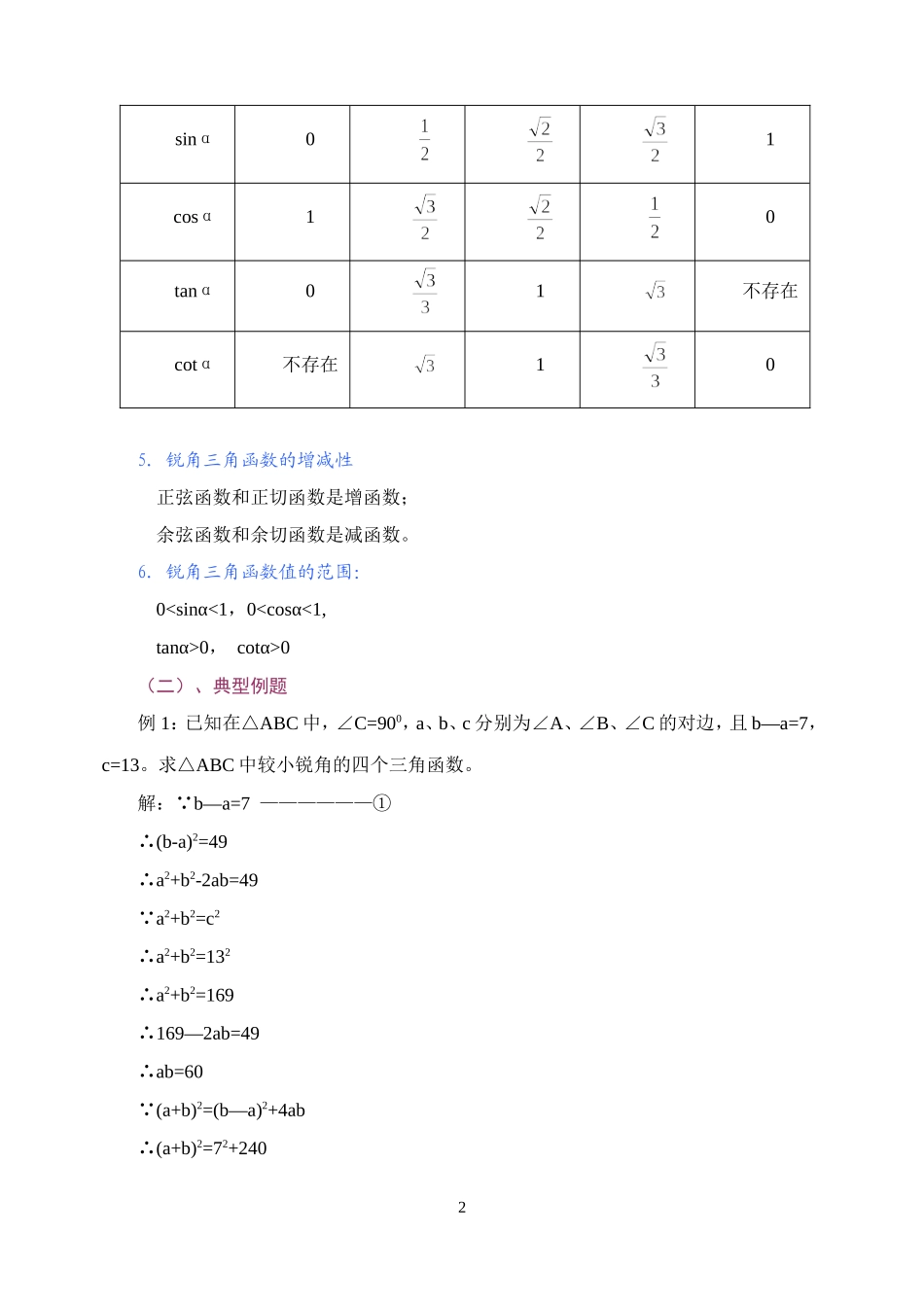
第十四章解直角三角形一、锐角三角函数(一)、基础知识1.锐角三角函数定义。在直角三角形ABC中,∠C=900,设BC=a,CA=b,AB=c,锐角A的四个三角函数是:sinA=,cosA=,tanA=,cotA=这种对锐角三角函数的定义方法,有两个前提条件:(1)锐角∠A必须在直角三角形中,且∠C=900;(2)在直角三角形ABC中,每条边均用所对角的相应的小写字母表示。否则,不存在上述关系2.同角三角函数间的关系:(1)平方关系:sin2A+cos2A=1;(2)商的关系:tanA=;cotA=(3)倒数关系:tanA=3.互余两角三角函数间的关系:sinα=cos(900-α)cosα=sin(900-α)tanα=cot(900-α)cotα=tan(900-α)通常我们把正弦函数和余弦函数叫做互为余函数,即正弦函数是余弦函数的余函数,余弦函数也是正弦函数的余函数,同样,也把正切函数和余切函数叫做互为余函数。上面的四个公式,就可以概括成一句话:一个锐角的三角函数等于它的余角的余函数。4.特殊角的三角函数值:003004506009001sinα01cosα10tanα01不存在cotα不存在105.锐角三角函数的增减性正弦函数和正切函数是增函数;余弦函数和余切函数是减函数。6.锐角三角函数值的范围:00,cotα>0(二)、典型例题例1:已知在△ABC中,∠C=900,a、b、c分别为∠A、∠B、∠C的对边,且b―a=7,c=13。求△ABC中较小锐角的四个三角函数。解: b―a=7——————①∴(b-a)2=49∴a2+b2-2ab=49 a2+b2=c2∴a2+b2=132∴a2+b2=169∴169―2ab=49∴ab=60 (a+b)2=(b―a)2+4ab∴(a+b)2=72+2402∴(a+b)2=289 a+b>0∴a+b=17——————②由①、②:a=5,b=12 a0∴b∴cosA=解法二:3 sinA=tanBtanB=cotAcotA∴sinA∴sin2A=cosA sin2A+cos2A=1∴cosA+cos2A=1∴cos2A+cosA―1=0∴cosA cosA>0∴cosA,说明:解法一是根据锐角三角函数定义求cosA的值,即求的值,解法二是利用c三角函数间的关系,建立关于cosA的一元二次方程,从而求出cosA的值,解法一是基本的解法,解法二具有一定的灵活性,对于培养同学的解题能力有好处。例3:已知cotα+=5,00<α<900,求cosα的值。解: cotα+=5∴+=5∴cosα+1=5sinα∴(cosα+1)2=25sin2α∴(cosα+1)2=25(1―cos2α)∴26cos2α+2cosα―24=04∴13cos2α+cosα―12=0∴(13cosα―12)(cosα+1)=0 cosα>0∴cosα+1>0∴13cosα―12=0∴cosα=说明:本题的条件中没有说明α角在直角三角形中,所以不能通过边的比求cosα,只能利用有关的公式建立关于cosα的方程,从而求出cosα的值。例4:比较cos230,tan230,sin230,cot230的大小。解: tan230cos300=∴tan2301∴cot230>cos230∴sin230cos300=∴tan2401>cos250∴sin230